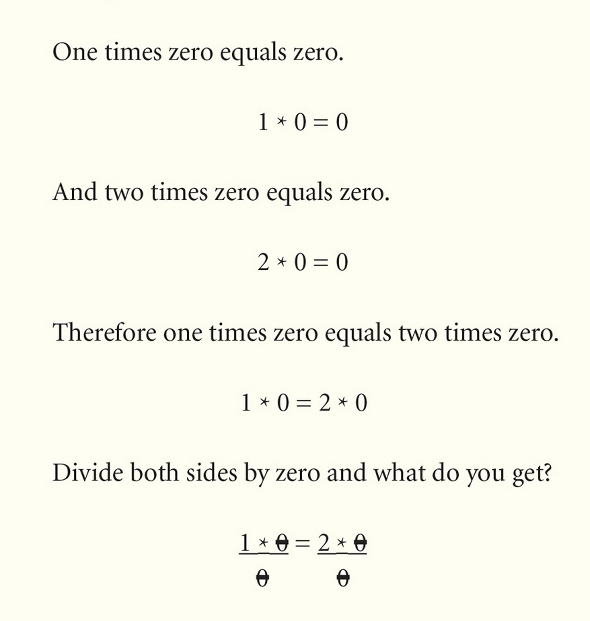“I’m nothing but numbers. Zeros and ones.”
TF-Narcon9
“How many raindrops?”—Caught in clogged traffic in downtown Los Angeles, Xanther watches the start of a torrential downpour from inside the car and ponders how she could even begin to count them. Although it initially appears to be an act of innocuous pastime, that question is, for Xanther, not entirely a matter of curiosity. Right at the outset, it becomes evident that, in fact, counting makes her highly uncomfortable: “Xanther shifts in her seat. Adjusts her glasses. Numbers make her uneasy. Math especially” (TFv1 50). That feeling of uneasiness even provokes many physiological reactions: she feels compelled to “scrunch her nose” (TFv1 50), “grip her seat belt” and “clamp [her] teeth tight” (TFv1 67). Despite the Sisyphean hopelessness of adequately and conclusively determining, let alone verifying such a number, Xanther cannot refrain from repeatedly engaging with it until she suffers a seizure. This opening scene, which I will prepare to discuss in more detail, not only introduces Xanther, for whom the pleonastic title “main protagonist” is in this special case felicitous, but also a balance shift in Danielewski’s writing inaugurated in the first season of the colossal project The Familiar, namely one from the topological to the arithmetical.
In general, The Familiar tracks cultural, scientific, techno-mathematical, and, in Xanther’s case, psycho-epileptic ramifications of numbers and digits, in approximately the same breadth and depth Danielewski’s debut novel House of Leaves investigates geometrical, social, and psychological topologies, negotiated on both the diegetic level of the house on Ash Tree Lane and on the metanarrative level of the page itself. What is especially salient is that The Familiar is dealing first and foremost with staggering numbers, of which Xanther’s name is somewhat indicative: exponentiation as in X to the nth power (Xn) escalates quickly into uncontainable magnitudes. Surely, this shift from the topological to the arithmetical is a matter of continuity rather than discontinuity, since House of Leaves itself is replete with numbers if only for the footnote count. Rather, Danielewski’s arithmopoetics, his specific writing of and with numbers, together with the incredible range of topics addressed and expressed by the numerical, is somewhat more pronounced and weighted but still ubiquitously in symbiosis with his hallmark topopoetics, his writing of spaces in and on the material page. That is why many crossover comparisons to Danielewski’s past work promise an apt introductory conceptualization of his arithmetic. We shall see that the arithmopoetical dimension of The Familiar not only adds to but in fact complements his predominantly topological oeuvre, a phenomenon especially salient in those instances Danielewski himself calls “signiconic.” The fact that Danielewski constantly brings together topological and arithmetical topics is evidence of him being a profoundly mathematical writer.
It is therefore warranted to speak of a “balance shift” from the topological to the arithmetical because several story arcs in The Familiar exhibit a metaphysics of number rather than a metaphysics of space that characterizes House of Leaves. In fact, let me cite two examples to not only set the stage but also reveal a direct transformation from the spatial to the numerical. First, one of the key premises in House of Leaves is the fact that the “width of the [Navidson’s] house inside would appear to exceed the width of the house as measured from the outside by ¼″” (HoL 30). This marks a geometrical paradox, insofar as the “outside” of a space cannot exceed the “inside” in size. The Familiar also discusses a mathematical anomaly, namely the arithmetical paradox that 1 = 2 (TFv1 59-60, 771; TFv5 214). It is one of Danielewski’s hallmark characteristics to imbue these paradoxes with a specific meaning, such that they transpose into uncontestable truths within the diegetic worlds in each novel. As with House of Leaves, the arithmetical paradox featured in The Familiar fuels the narrative and—as I shall argue—constitutes the lynchpin of the entire first season. Furthermore, these two paradoxes also showcase the previously mentioned balance shift from the topological to the arithmetical in that the former pertains more to a spatial measurement, whereas the latter is rather concerned with the laws of arithmetic. Second, let us take into consideration “The Five and a Half Minute Hallway,” an ominous “dark doorless hallway which has appeared out of nowhere” (HoL 57), featured in The Navidson Record in House of Leaves. The hallway is a flagrant spatial anomaly, insofar as the Navidsons traverse this space without being able to discern it from the outside. Strikingly, the specificity of “5 ½” is so conspicuous that it appears to be directly translocated into The Familiar, as it designates the duration of Xanther’s status epilepticus, which lasts “5:33” (TFv1 254), a duration very close to “5 ½” minutes. The makeup of these pages (cf. TFv1 242-54) showcases the novel’s emphasis on a numerical poetics as the numbers are arranged in circles to simulate elapsing time, prompting the reader to count the minutes and seconds. This motivates not only the present hypothesis that the reader witnesses a smooth shift from topopoetic to arithmopoetic strategies, but it also alerts us to pay heed to the specificity of numbers.
Not least because of the familiarity between arithmetic and topology as branches of mathematics, this marriage of “number” and “space” in The Familiar will not seem strange to a reader of Danielewski. On the contrary, it feels familiar. Sascha Pöhlmann has highlighted the aspect of recognizability of Danielewski’s work, stressing that “one can only be amazed at the fact that Only Revolutions and House of Leaves are instantly recognizable as Danielewski’s works at first sight but at the same time could hardly be any more different” (“Democracy” 1–2). Pöhlmann’s statement is crucial insofar as it holds perfectly true for The Familiar as well. For this specific case, it is—amongst the rather obvious Danielewskian predilections, such as coloring the central word of the title—the examination and negotiation of the number with spatial conceits that enshrouds the reading experience with a looming sense of familiarity. At the same time—and the second part of Pöhlmann’s statement alludes to that as well—“space” and “number” trigger associations so different from each other that they could hardly be more divergent in conceptual and philosophical terms. Though that is the crux of the matter: the condition of being alike or similar while retaining facets of difference immediately points to the act of counting, since counting can only aim at and group together what is similar, yet unidentical—in short, familiar.
Danielewski’s Arithmopoetics: Exorithmetic, Endorithmetic, Mesorithmetic
In Danielewski’s work, numbers are identifiable on three different narratological levels: first, they play a significant role outside of the story, namely in the material makeup of the project and its numerical organization in a series of seasons, volumes, acts, and chapters; second, they occur inside of the story, as characters explicitly think about and with them, not rarely making them the topic of highly compelling discussions; and third, they function as a dimensional glue for narratological recursions typical for Danielewski, in that the number becomes the mirror in which the exteriority of the volumes, the hardware, is reflected in the story itself, the software, and vice versa.
Usually, these levels operate, by definition, independently on separate planes of discourse; many critics agree, however, that Danielewski’s work is characterized precisely by their entanglement. For example, in his reading of House of Leaves, Ridvan Askin adopts Deleuze’s concept of the fold to argue that the novel features “a house where matter and soul permeate both levels” that “irreducibly fold onto each other” (103). As the convoluted array of footnotes and miscellaneous appendixes replicate the labyrinthine topology of the house, the reader actively partakes in this folding operation, since “the novel makes the reader part of its telling by making her constantly decide which section to continue reading” (103). In other words, Danielewski’s typographic break of linearity transposes reading into an act of navigation, where reading and walking the labyrinth occur simultaneously and map onto each other, such that “the reader forms a fold with the novel” (104). Such an amalgamation of “inside” and “outside” is also diagnosed by Julius Greve, who, with regard to the novel’s overtly self-conscious makeup, claims that “the location of the outside is called into question as the concept of metacommentary enters the aesthetic realm. The function of this former externality is now folded into the work of art, enclosed within its domain” (87). Greve’s insight is that it is usually incumbent on the “outside” to provide commentary and criticism on the novel’s “inside;” the novel, however, sabotages such a clean separation by emulating that “outside” criticism from within. Finally, analyzing the geometrical fabric of House of Leaves, Hanjo Berressem similarly contends that Danielewski “fundamentally deconstructs the spatial categories of inside and outside” with recourse to the emergence of a “one-sided projected plane” (211). In other words, in projective geometry, a transcendental position outside of the plane, as exemplified by Euclidean geometry, is prohibited. Berressem’s mathematical argument congeals with Askin’s argument of the fold and Greve’s argument of the metacommentary-from-the-inside, in that any clean inside/outside categorization is complicated by the fact that the act of reading the novel from the “outside” necessarily produces a twisted and tangled relationship with the novel’s interiority. Thus, when it comes to analyzing Danielewski, the measurer is always part of the measurement.
The critical consensus outlined above alerts all subsequent criticism to pay heed to the “how” in Danielewski, because, in his work, the “how” has never failed to complement and intensify the “what.” Often, the “how” from his earlier novels entails a predominantly spatial manipulation of text, of which the labyrinthine replications previously mentioned are important examples. However, such topological transformations are considerably less pronounced in The Familiar, albeit not entirely conceded. Surely, the chapters of all nine protagonists display different patterns of textual arrangement that somewhat reflect their character traits: Jingjing’s text, for example, coupled with the rather informal and curvy-looking font “Rotis semi sans,” often formlessly exhausts the spatial capacity of the entire page, exposing his hedonistic, abrasive, and talkative side, while Isandòrno’s text, written with the sharp-looking “Visage” font, marks the radical opposite, as it is always contained in a neat, small, perfect rectangle and planted right in the middle of the white nothingness of the page, accentuating his silent, cold-blooded, unassuming, accurate, dutiful side. In comparison to House of Leaves, however, a quick perusal confirms that such topological conceits are reduced both in number and intensity.
Because The Familiar maintains a remarkably stable structure in all five volumes of the first season, the somewhat receding topological idiosyncrasies allow a numerical aesthetics to come to the fore. With respect to the three domains of inquiry mentioned above, the outside, the inside, and the in-between, the pending arithmopoetical analyses pertaining to each level could be called exorithmetic, endorithmetic, and mesorithmetic. This triad is rather loosely based on the three Aristotelian distinguishing features of all art or “modes of imitation” in his Poetics: means, objects, and manner. For Aristotle, means are the different media that produce “rhythm, language, and harmony—used, however, either singly or in certain combinations” (2316), while objects “are actions, with agents who are necessarily either good men or bad” aiming at the “diversities of human character,” and manner means quite straightforwardly the way “in which each kind of object is represented” (2317). According to this terminology, then, the means of The Familiar points to the materiality of the narrative and its specific rhythm or “meter” of serialization, its objects predominantly involve the lives of the nine protagonists—I will focus on Xanther, Anwar, and Dov—and its manner aims at the representation of these nine characters’ lives by the narrator TF-Narcon9. TF-Narcon9 is ostensibly deeply involved in their thought processes, but still not deep enough to warrant the use of the first-person pronoun “I” since each chapter is narrated in the third person singular. Danielewski’s work can thus be located at the threshold between mimesis (art by presentation) and diegesis (art by narration): the characters’ actions are indeed narrated by another agent, but from an infinitely proximate vantage point, from an “inside” that presents itself to the only barely “outside,” reflecting once more their conceptual entanglement so typical for Danielewski’s novels.
In the first section on Danielewski’s exorithmetic, I will analyze how numbers play a role in the design of the serial novel. It is conspicuous that Danielewski’s strictly numerical format is relatively stable across the entire first season, which prompts questions with regard to the rationale behind those numbers. Relying on a section of The Truth in Painting (1987), in which Jacques Derrida attempts an equally dangerous and eerily familiar enterprise, I provide a possible interpretation of Danielewski’s choice to publish 27 volumes. As this is a truly voluminous endeavor, I argue that this serialization requires a specific habitus of reading that is different from those Danielewski’s novels previously required. In that way, Danielewski’s oeuvre is truly unique as it introduces a field that could be called exomechanics of reading.
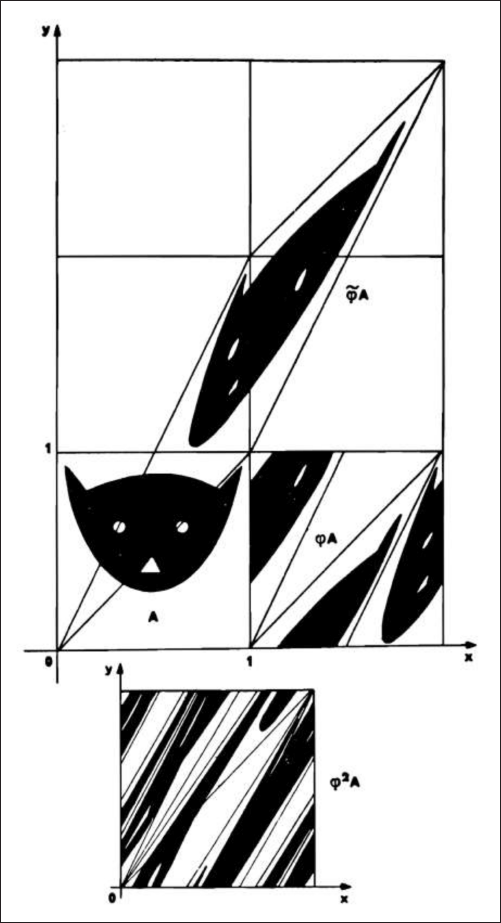
In the next section, I tackle the issue of Danielewski’s endorithmetic. The exonumbers from the previous section have already revealed The Familiar’s tendency to be governed by large numbers; in light of this, it is not surprising that we shall find many large numbers—staggering numbers as some characters will call them—in the novel itself. These staggering numbers occur primarily in the contexts of rain and raindrops, money and bookkeeping, and information technology, provoking metaphysical and mundane questions alike. In many instances, these numbers are overwhelming for both the characters in the novel and us readers. With a view to conceptualizing this “overwhelmingness” (TFv1 61), I will introduce Immanuel Kant’s theory of the sublime. Based on Kant’s terminology, I aim to show that Danielewski’s signiconic depiction of rain in the first volume introduces a transition from the mathematically to the dynamically sublime. The mathematically sublime does not in principle preclude the prospect of counting raindrops; the reason why it invokes a sense of overwhelmingness is rather the colossal result of such an undertaking. However, through multiple signiconic techniques, the raindrops become gradually “muddier” and hence truly uncountable, giving way to an aesthetics of velocity and violence that classifies the dynamically sublime. Through our main protagonist Xanther, we will not only wrestle with such difficult problems of countability and muddiness but also witness how her epileptic attacks are connected to them. I will argue that her epilepsy is portrayed as a response to the rapid oscillation between form and chaos, understood as the countable and uncountable side of the world. Her predicament also has a psychoanalytical dimension, which I shall elucidate by examining her relationship with Dov, her biological father. I will then contrast these findings with Danielewski’s depiction of Anwar’s trauma through “Arnold’s cat map” (TFv5 739), distilling meaningful differences between the epileptic and the computational. This may explain Xanther’s temporary relief from her epileptic attacks after she accepts an uncomputational idea as a token of truth, namely the paradoxical equation “1 = 2,” which could be considered the “catsum” (TFv1 67) of the first season.
The last section will deal with Danielewski’s mesorithmetic. I will combine the exonumbers as presented in the first section with discussions on endonumbers in the second to arrive at conclusions to all arithmopoetic speculations, which is in many ways a feline arithmetic. Here, I will also discuss the numbers of the Narcons, the enigmatic narrative agents positioned right at the threshold between form and content. An outline of the basic idea behind a recursion as it is used in computer science will illuminate both their function in the novel and their relationship to numbers as well.
Exorithmetic: Seriality and Format
It is striking that Cas’s description of her writing a series of books as a young computer scientist is largely analogous to the evolution of Danielewski’s The Familiar:
TFv1 151.1
Danielewski told NPR’s Arun Rath that the project “began very much like the little creature that Xanther finds as this tiny, sleeping, near-moribund thing” [“The first apparition had seemed so small, nearly trivial. A dash of words, some numbers, no more than a few lines at most”], but “then began to awaken in a way that surprised me. And I thought, it could be two books, could be three. […] I began to see that it was a much larger work” [“quickly evolving into a book, and then books, volumes on how it all worked, or rather revealed itself”], until he had “10 volumes. But in writing the tenth, I […] understood intimately how to re-write the first” [“the paragraphs had stretched into pages until the formulae were rewrapping themselves to the beginnings”], thus logically spending “a long time with my books. […] This one has been in the works for nine years” [“eventually spending years struggling with the errata”]. This parallelism between Cas’s volumes and those of The Familiar not only bespeaks a metafictional inside-outside-convolution as previously mentioned, but especially the use of words such as “numbers” and “formulae” point to the prominence of the arithmetical. Moreover, it also provokes tempting hypotheses regarding authorship and its role and negotiation in the novel. Did Cas program the Narcons? Also, her husband Bobby’s statement that “the Distribution went everywhere. Self-replicating. Mutative to the point of dissuading identification but not to the point of compromising content” (TFv1 144) could in fact allude to the workings of the printing press that publishes, reproduces, and distributes the serial novel.
The last sentence in Cas’s quote reveals that she had invested a lot of time in designing a “vast infrastructure and signal exoskeleton to gather the inputs and support the rendering” for her book series. Again, assuming more than just an aleatory correspondence between Cas’s and Danielewski’s modus operandi in creating a serial work of science/art, the erection of an “exoskeleton,” or, in other words, the implementation of a serial format, unequivocally falls into the remit of Danielewski and must constitute a substantial time-consuming engagement for him. The fact that the format has been stable over the course of the first season suggests that it will persist in the coming seasons and promise a semantic dimension as well. As it is predominantly numbers that are in display in the serial format, I will investigate how they govern and uphold the structural matrix of the entire The Familiar franchise—to borrow Cas’s terminology, its exoskeleton—and as such, the following analysis aims at the Danielewskian exorithmetic.
The format of volume one, One Rainy Day in May, is replete with numerical invariants, which have set a structural precedent that all subsequent volumes have hitherto adhered to. Featuring 9 main characters, each volume contains exactly 880 pages and is divided into 30 chapters, which are in turn organized into 5 acts, each comprising 6 chapters introduced by 5 artful double-page Entr’Actes. In the aforementioned NPR interview, Danielewski divulged that The Familiar was planned to be “27 volumes long” (NPR). If that plan were realized, the total page count by the end of the project would amass a staggering 27 × 880 = 23,760 pages, including the many previews and final sequences that take up approximately 100 pages of each volume.2 Unlike the serial format’s rigidity, the individual chapters themselves do not follow an obvious pattern; also, the distribution of the chapters within each volume is not openly formulaic or explicitly regulated, hinting at an inkling of chaos within the arithmetic strictures.
Consequentially, if we agree that these numbers (9 characters, 30 chapters, 880 pages, 27 volumes) are neither whimsically chosen nor randomly generated, what meaning or rationale could they codify? First, on a general level, we can surmise that the total volume count of 27 is within the proper range of what could be called “serial practicability.” Given Danielewski’s assessment that The Familiar resembles the structure of a full television series,3 27 volumes are within a realistic range to be divided into approximately 5 × 5 seasons; the hypothesis that each season packages exactly 5 or a comparable number of volumes is corroborated by the first season’s precedent. Also, in the NPR interview Danielewski provides a preliminary list of successful TV series that have told “a story in much greater detail and with much greater patience,” namely “The Wire or the wild speculations of Battlestar Galactica. Certainly Mad Men, certainly The Sopranos, certainly Breaking Bad,” all of which are, by and large, of comparable length. They promise an apt dramatic equilibrium in approximately 5 seasons as they are not too short to collapse into the duration of film, and not too long to suffer from dramatic laxity, as is often the case for TV series with a double-digit season count. What is more, Danielewski mentions the number 5 as in “the five seasons of The Wire,” which evidences that he considers the overall runtime of these series as well. Nonetheless, this may perhaps satisfy the scope of the project, but it does not entirely explain the reasoning behind the set number 27. Danielewski’s certainty about the definitive length of his project is truly remarkable in this regard. As the reporter asks him “What are you doing these days?” Danielewski resolutely answers “I’m writing a novel. […] It’s 27 volumes long.” Again, then, the question pertaining to the particularity of 27 is looming: why exactly 27? How can Danielewski be so fastidious about the count after reportedly only having finished season 2?4
This fastidiousness regarding the 27 refuels the urgency to pursue meaning behind this figure. Again, the traditional argument that looks at Danielewski’s previous modus operandi prompts the same undertaking. His novel Only Revolution irrefragably testifies not only to his proclivity for numerico-geometrical experimentation, but also to his tenacity to cultivate the entirety of his writing under arithmetic constraints. Hanjo Berressem rightly speaks about “a conceptual rigor and mathematics in Danielewski’s poetics” (213), providing an exemplar of such an analysis by counting the lines and pages:
[Only Revolutions] has 360 pages, and each half page consists of 36 lines and 90 words, which adds up to 180 words per page and 360 words for the two pages of the opened book. This structure is a perfect example of how constraints create concepts: not only does the structure quite obviously relate to the 180° revolutions that define the reading process, one might also think of each page of the two ‘books’ combined as a longitude (one degree of the 360 degrees of the global network of meridians) and of a page of each single book as a latitude (one degree of the 180 degrees of the global network of parallels). (200)
With Berressem’s analysis in mind, Only Revolutions operates at the threshold where geometry and arithmetic “kiss” and produce poetry; it is a novel about a “familiarization” of these fields. This attests that Danielewski’s numbers are heavily loaded with meaning at least in one major case. This precedent of Only Revolutions legitimizes the inspection of the numerical format of The Familiar as well, especially because it displays comparable numerical fixations. Admittedly, however, a cursory glance over The Familiar shows that counting lines, for example, will not yield such a straightforward result, since many pages, also those within the same chapter, comprise an ever-alternating number of them. The elegance in the numbers addressed in Berressem’s analysis partly derives from the unshakable correspondence between the numbers 36, 90, 180, and 360 and the geometrical properties of the (half-)circle. Such a correspondence is disproportionately more difficult to establish for The Familiar, as, for example, the number of chapters (30) does not divide the number of pages (880) without a remainder. Since the numbers in Only Revolutions pertain explicitly to the geometry of the circle, they effectively function as a stable structuring principle, whereas the numbers in The Familiar do not follow such a straightforward pattern.
To tackle this question of the exorithmetic in The Familiar, then, we will engage in what Jacques Derrida fittingly calls “arithmopoetic speculations” (208) in The Truth in Painting. Investigating serial art, which designates the completion of a singular artwork by the combination or summation of a subset of numbered artworks, Derrida is in a comparable situation, asking himself whether the artwork’s specific serial count be inherently meaningful and relevant, regardless of the artist’s intentions. Correspondingly, just as a reader of The Familiar might be intrigued by the 27 volumes, Derrida is intrigued by the 127 coffin drawings in Gérard-Titus Carmel’s The Pocket Size Tlingit Coffin (1976)—and a scrutiny of Derrida’s method will prove beneficial for our present analysis. His third chapter, “Cartouches,” constitutes a prime example of an “arithmopoetic whodunit,” trailing the significance of the number 127 and testing its qualities from various angles. Derrida logs his ruminations, stream-of-consciousness style, in the form of diary entries, allowing us to infer that he grapples, sometimes quite desperately, with the question for over 42 days (from November 30, 1977, to January 12, 1978). On December 6 he begins his avid investigation: “Coming back […]—127 times. […] For the moment, this figure—127—says nothing to me” (193); two days later, on December 8, he again inquires: “How to give a reason for this ration, the 127 for example?” (200) Later, on the same day, shortly after asking himself “Why the death sentence [l’arrét de mort] at 127?” he confesses: “Things won’t stop computing in me, as if I wanted to account for [rendre raison de] the number, give a pertinent reason for the contingent ration” (204). The word contingent perfectly captures our predicament as well, because Danielewski’s 27 fixates a contingent, a “quota,” while simultaneously lacking an obvious rule or algorithm, ergo being uncertain; it is, as of yet, “contingent” in both senses. Derrida’s methodology presents the intention behind all “arithmopoetic speculations”: it aspires to read numbers in context and attempts to imbue them with meaning. Thus, we can follow Derrida’s succinct chiasm that all arithmopoetic speculation is a quest to give “pertinent reason for the contingent ration.”
Unable to move forward, Derrida browses the presence of the number in Titus-Carmel’s earlier artworks, many of which are serially composed as well. The 34 in the “34 drawing of The Four Season Sticks” (205) prompts Derrida to calculate their arithmetical interdependencies: “3 × 4 = 12, 3 + 4 = 7, 12 and 7: 127.” Note that we have adopted Derrida’s heuristic too: we have consulted the numbers in Danielewski’s earlier work, namely Only Revolutions, in order to reveal the artist’s attitude regarding numerical expression. In our example, we must resign before the incompatibility between the numbers of Only Revolutions and The Familiar. So must Derrida, initially; but on December 9, after a few more scribblings, “127: 12 + 7. 12 = 3 × 4 (hours, months, seasons, anything at all, you choose), 7 = 3 + 4 or again 1 + 2 + 3 + 4 = 10 and 1 + 2 + 7 = 10. Pythagorean tetractys” (208), Derrida serendipitously stumbles over a helpful gadget: “This morning, on my table, I’ve a little ‘electronic pocketable calculator’ (model Ur-300, serial no. 27932) next to the typewriter. I compute, with a somewhat distracted hand. And here it is: 127 is a prime number” (208). For Derrida, this discovery is momentous, insofar as the number’s primality undergirds his theory of seriality as being “one” and “many” at the same time, a hermetically sealed entity that is nonetheless internally plural: “A prime number, by definition, is only divisible by itself. By no other whole number. The coffin, in its generic unicity, is thus entire, intact, invulnerable, divisible by nothing other than itself. Nothing will affect it again from outside” (208). Derrida’s word choice is important, because it shares an important characteristic with Danielewki’s: Derrida writes in the singular, “the coffin,” as Danielewski, who also speaks about “the novel” in the singular, which is “27 volumes long.”
Danielewski’s 27, however, does not pass the primality test, although the numerical quality of primality would have been perfectly fitting for such a project as well. Also, there is a sense of confusion arising from the fact that 25 (= 5 × 5) would have been an orderly season count that would macroscopically reflect the microscopic internal division of each volume into 5 acts; it would have been a fractal structure. Hence, what is it that the 27 offers Danielewski that the 25 cannot? In the pursuit of an answer, Derrida’s tenacity with regard to solving the arithmetic problem should give us the courage necessary to arrive at another conclusion. With a pocket calculator on our own (mine is a TI-84 model, serial no. 2095003782 S-1104), or with quick recourse to mental arithmetic instead, the number 27 unequivocally hints at another aspect: Danielewski’s seriality is voluminous. 27 is a well-known cubic number, as it measures the volume of a cube with equal length, width, and height, as 27 = 3 × 3 × 3. Strikingly, Danielewski’s desire to “tell a story in much greater detail and with much greater patience,” which entails a spatial dilatation in order to adequately address the individuality and uniqueness of the characters, is both achieved through the 27-fold serialization of the novel and the oscillation between textual linearity and graphic depth, such that the novel gains volume over time. In direct comparison between the unique and the serial, one could even go so far as to say that all characters, especially if there is a great number of them, are necessarily doomed to remain somehow “flat” in novels, because a novel cannot offer the sprawling periodic snapshots with which their continuous development is revisited and thus becomes organic and tractable. Following that argument, the number 27 expresses precisely that: the count of characters (9) also tacitly slumbers in the 27 = 9 × 3. The 9 governs the “plane” of characters, the basis of the novel’s unfolding, initially restricted to the planar page. Upon a serial stacking into the third dimension, then, The Familiar becomes a truly voluminous endeavor, not least represented by the staggering numbers we will encounter in the section on Danielewski’s endorithmetic. Seriality grants them not only the liberty but also a wide developmental horizon, a new direction, to truly “unfold.”
In the third part of this essay on Danielewski’s mesorithmetic, I will finish these arithmopoetic speculations by addressing the specificity of these numbers, taking into account the character count (9), the number of chapters in a volume (30), and the number of pages (880). Drawing on observations I will present in the second part on Danielewski’s endorithmetic, I will show that these numbers all relate to a cat, testifying that the novel is structured according to what could be dubbed a feline arithmetic.
Exomechanics of Reading: Ergodicity and Materiality in Danielewski’s Novels
Against this numerical background, I want to briefly address one effect of Danielewski’s exorithmetic by touching on what could be called an exomechanics of reading, a concept that echoes the voluminous serialization of the novel. First, a discussion on the mechanics of reading may be helpful to apply the concept of “ergodic literature”—well-known in Danielewski studies—to The Familiar, albeit in a different guise. “Ergodic literature” is straightforwardly defined by Espen J. Aarseth as the requirement of a “non-trivial effort” to “allow the reader to traverse the text” (1). Some critics have diagnosed such a “non-trivial effort” in the perusal of House of Leaves. For example, Luka Bekavac confirms, with recourse to Aarseth’s typology, that the “layout” of House of Leaves “certainly presents a considerable material obstruction” (329) to a smooth reading, and he further cites “Chapter IX” as the most conspicuous example of ergodicity. Due to the confusing spatial manipulations of the text on the page, Danielewski relegates to the reader the responsibility and agency of processing the text in a meaningful manner. Doing so, the reader must partially deviate from the quotidian traverse from left to right and top to bottom. It is hence incumbent on the reader to maintain orientation in such entangled strains of narrative, multiple involutions of intra- and extradiegetic levels, and bombastic footnotes exceeding the length of manageability. Reading House of Leaves, we must forfeit the comfort of a true and original path, as there is none.
But is it possible to speak about a level of ergodicity with respect to The Familiar? I will propose an affirmative answer to this question, but a short glance at Only Revolutions is necessary to make the point. Although it may even be invalid to speak about “ergodic literature” in this case, the non-trivial effort needed to traverse the text does not necessarily consist of a cognitive one, as in House of Leaves, but rather of a mechanical one. The method of traversing the text is different: after having chosen either Sam’s or Hailey’s point of departure, the reading vector is not entirely fixed but, in comparison to House of Leaves, substantially more stable. Therefore, its main “ergodic aspect”—if there is one—is not an act of establishing a reading compass, because, regardless of the reader’s path, its ingenious construction predicts, quite beautifully, that Sam and Hailey will never leave each other because they always find each other, a circular logic that befits the pith of the story. Rather, the ergodic aspect is grounded in a different type of work performance: the revolution of the book, which Hanjo Berressem calls “revolutionary poetics” (205). A successful reading necessitates a “180° turning of the book” (217), which constitutes a rather unusual gesture that resembles the “turning of vinyl LPs on the record player” (217) and as such is threatened to become, qua technological advancement, a gesture of obsolescence. Thus, the “nontrivial effort” is primarily a cognitive one for House of Leaves and a mechanical one for Only Revolutions.
In mentioning Only Revolutions in this context, I do not wish to argue that the novel exemplifies yet another instance of “ergodic literature”; rather, I wish to point at the fact that Only Revolutions functions as a hinge between House of Leaves and The Familiar to highlight another aspect of ergodicity that is at play. First, as to The Familiar, reading complexity is admittedly largely attenuated. In contrast to House of Leaves, the text appears to be devoid of any convolutedness of textual hierarchy, for example, not least because of the visual demarcation according to the Narcons’ “Parameter 4,” which posits that “All Narcons are bracketed” (TFv1 574), explicitly revealing the (extra-) diegetic domains in play and, in theory, protecting them from any interference. Harking back to the critics’ consensus on Danielewski’s deconstruction of the outside and the inside, the Narcons’ bracketing, at least momentarily, reinstalls a conceivable threshold that simplifies the observance of narratological registers. However, the first season already signals the potential deconstruction again, because the Narcons openly violate their parameters and Xanther somehow seems to be able to infiltrate their protected domain. Nonetheless, in The Familiar, the reader is at least cognizant of the rules that are susceptible to be violated, whereas in House of Leaves, these rules are not even manifest.
Let me now briefly address the mechanical aspect with respect to altering the angle of reading. Although in The Familiar the reader is generally absolved from the imperative to rotate the novel, the rotations require considerably more mechanical effort than in Only Revolutions or House of Leaves. Rotations are necessary for the introductory previews, comprising, inter alia, VEM primers and Caged Hunt videos in each volume, as well as the occasional graphic interspersions. Yet, the mechanical effort necessary is higher than in the preceding novels due to extraordinary difference in weight: a single volume of The Familiar weighs 1655 grams,5 versus a copy of Only Revolutions only weighing 571 grams and a copy of House of Leaves weighing 1044 grams.6 Also, the volume of each volume is larger than Only Revolutions and approximately equal to House of Leaves but, partly due to the protruding cover, considerably less handy, which makes a rotation of a copy of The Familiar a rather uncomfortable act. These numbers moreover reflect—and partly condition—the habitus of reading. As a road novel, Only Revolutions almost begs to be taken and read on the road, especially because Danielewski’s construction resembles an incredibly organized suitcase, in which 360 pages are miniaturized and “packed into” 180. As a house novel, the materiality and the largeness of House of Leaves, on the other hand, suggests a reading at home; one could technically still take it to bed, as it permits a critical reading from a supine position. As a desk novel, the heaviness and voluminousness of The Familiar almost demands to be read at a table. Accounting for the critic’s indispensable readiness to wield multiple volumes of the novel to establish overarching references, The Familiar cannot be easily taken to bed. Rather, its physics nudges the readers to traverse the novel from a sedentary position. Aesthetically, the numerical voluminousness of the novel, going hand in hand with its mass, reflects the longevity of the characters and the grandeur of the entire project, as multiple volumes are either spread or stacked on the table. This shows that for Danielewski’s novels the exomechanics of reading are by no means negligible but point to truly “non-trivial” concessions and preparations necessary for a careful and discerning perusal. Here, I must perhaps ask the interested reader to either admit or rebut whether it occurred to them that they have sometimes, despite their critical appetite for literary complexity, opted to forego the inspections of the numerous Narcon references that redirect to earlier volumes on the account of the volumes being so incredibly heavy. The path of least resistance dictates a swift and uninterrupted adherence to the series’ comfortable chronology, whereas a disciplined consideration of each cross-reference produces a diegetic knot with measurable physical gravity. This overwhelming weight of the novel as a token of its materiality not only mirrors the voluminous exonumbers but also maps onto the staggering numbers featured within the novel, which we will discuss now.
Endorithmetic: Numbers, Epilepsy, and the Cat-sum
What I call endorithmetic denotes the arithmetical poetics from within the novel, and I will use the term to investigate how numbers are generated, portrayed, and negotiated by the characters. I previously mentioned the introductory scene of Xanther trying to count the raindrops, and that scene elucidates so many elements regarding Danielewski’s complexification of numbers and their projections onto the page that it serves as an optimal springboard for the present discussion. To conceptualize Danielewski’s portrayal and discussion of numbers in multiple contexts, I shall integrate the concept of simultaneity into the present line of argument. While the exorithmetic dimension is strongly regulated by numeric seriality in the form of succession, Danielewski’s techniques invoke a hybrid between seriality and simultaneity in the form of the signiconic. Furthermore, the endorithmetic portrayal elicits psychological insights of the characters, especially Xanther; therefore, while the exorithmetic accomplished paradigmatic and constraining objectives, the endorithmetic reifies the psychology of Xanther.
On the tenth of May 2014, a Saturday, Anwar and Xanther are on their way to multiple destinations: first, Xanther has an appointment with her psychologist Dr. Potts, then Anwar takes her to his workplace at Square One, and after that, Anwar and Astair want to surprise Xanther with a dog. The rain becomes increasingly torrential as the two follow their schedule, and predictably, their planned itinerary derails into an odyssey. The first image we have of Xanther is her pondering the count of raindrops, an almost impossible endeavor that is even detrimental to her health. In order to convey and at the same time intensify Xanther’s depressed feeling, Danielewski uses a well-established method from his repertoire to render her predicament more visceral to the reader. Aligned diagonally, the letters of “How many raindrops?” limn the contours of falling raindrops in real time: the growing surge of the rain is, as the chapter progresses, spatiopoetically captured by lines of text diminishing in size while multiplying in number. At first, the droplets are thick and countable and only occupy a single page (TFv1 49, 51, 55), and then they become gradually more difficult to count, occupying several pages (TFv1 62-65), until they become so small and multitudinous that any act of counting is rendered practically unfeasible (TFv1 78-79). This projection makes the reader see the downpour through the eyes of Xanther, who, in turn, sees in the droplets a tantalizing math exam she is doomed to fail from the start. The fact that the raindrops are composed of words contributes to the realism of Xanther’s psychical state, because in them lingers a mysteriously compelling imperative to number them.
Multiple mechanisms are at play that are conducive of potentiating the reader’s empathy with Xanther: the depiction of rain decelerates the reading tempo because the raindrops call for a reading, and from page 62 onward, they transform from the simple “How many raindrops?” to metaphysical questions. Also, the diagonal text demands a slight rotation of the heavy volume to process the entirety of information. The gesture of the tilting head over a slightly rotated novel on the part of the reader is emblematic of the situation, insofar as we share the compulsion to “read” each single raindrop, which mimics Xanther’s compulsion to “count” them. These processes are synchronized as they unfold simultaneously in “real time.” Furthermore, the reader’s unwillingness to “read” each raindrop—which results in some form of fatigue or resignation—maps onto Xanther’s exhaustion with this “deluge” of information.
The feeling that dominates the scene is surely not foreign to Danielewski studies: claustrophobia. The fact that the “raindrop-pages” recur several times and intermittently perturb Xanther’s conversation with her father add to her annoyance, uneasiness, and ultimately to the ineluctability of the questions, growing not only in force but also in weight. That is why the reader readily relates to Xanther’s self-diagnosis in feeling “like some caged animal” (TFv1 52), by witnessing first-hand how the lines of “How many raindrops?” become the bars of her mental cage. In many respects, Xanther’s feeling in this situation, enclosed in a car, surrounded by cars on all sides in a traffic jam, barred down by unanswerable questions and haunted by the “ghost in the raindrops” (TFv1 66) indeed justifies her feeling locked in. On top of that, it offers a psychological explanation for her unwavering alliance with animals of all kinds and her mission to free them of their cages wherever she encounters them.
Before venturing deeper into Xanther’s psychology, I want to examine some profound questions on the ontology and epistemology of numbers that are raised by her curious mind. It is striking to observe how rapidly the acuteness and philosophical depth of her questions increase over the chapter. Initially, Xanther thinks that rain might be a “figure without a number, maybe without a name” because “maybe, that’s what rain means? a number that’s a number that stays unnamed?” (TFv1 50). Quickly, her “head is a fog” (TFv1 53) after she starts to conflate letters with numbers: “Is that an E or a 3? […] M too? Or was it W? 13? 31? Def 3. Maybe 8? Z?” (TFv1 53); and even question words she cannot help to count “What – When […] – Why. Plus How. Nine + one. Ten. Like fingers and toes. Like numbers” (TFv1 56). As the rain grows stronger, Xanther submits to the ensuing question battery: “What kind of counting equals this sort of overwhelmingness? Does one gallon of water even have the same number of drops as another gallon? Or are no two drops ever alike? Like snowflakes? Like, there must be big ones and little ones, right? Except when does too big count as something too big for the word raindrop? Or too little?” (TFv1 61) This series of questions then cascades into the cardinal ontological one: “What’s that number? It has to exist, but if no one will ever name it, is it ever real?” (TFv1 61). It is almost unthinkable that a twelve-year-old girl, regardless of how much “she and Anwar Wiki […] trying to answer as many questions as possible” (TFv1 57), asks such infinitely profound questions that revolve around the entire complex of counting. As a matter of fact, the questions continue for quite some time after that, each of them as valid, interesting and, most of all, mind-bendingly difficult as the other.
What Danielewski correlates here is the count of raindrops and the nature of questions in general. In the same vein that Anwar teaches Xanther “in his mild and quiet manner how not all questions are the same” (TFv1 56), Xanther rearticulates the question with regards to raindrops, asking if they are the same or different, tapping into the ancient tradition of the one-many problem posed by Zeno in Plato’s Parmenides. Danielewski’s portrayal of raindrops as carriers of questions pictographically shows how Xanther wrestles with the question by redirecting Anwar’s insight onto a new phenomenon. A question that is raised by Zeno and reiterated by Socrates shows the familiarity of their inquiry: “[I]f things are many, they must then be both like and unlike, but that is impossible, because unlike things can’t be like or like things unlike?” (Plato 361). Socrates swiftly resolves this conundrum by showing that likeness and unlikeness are not mutually exclusive, in that “things that partake of both of these have both properties, there seems to me nothing strange about that, Zeno” (363). For Socrates, numbers must exist because of the following chain of reasoning: “’[W]e can say ‘being’?’—‘We can.’—’And, again, we can say ‘one’?’—‘That too’” (377). That is how Socrates derives the existence of “2” since there is “being” and “one,” which are different from one another and thus can be counted as a pair.
The example of Parmenides is surely edifying with regards to how the parts of a single whole invoke the concept of number. However, it does not apply to Xanther’s example, because it is evident throughout the treatise that Socrates refers to a rather static form of being, in which counting may be an enervating but foremost a feasible enterprise. For Xanther, one of the most elementary problems is connected to the de facto infinitely short travel time of raindrops from the clouds to the ground: “[H]ow quickly would she have to move to account for each topping wobble of wet? Of course, she couldn’t move fast enough. No one could. What could? […] What about all the drops forming and reforming in the in-between?” (TFv1 60-61). Arguing with Gottlob Frege, the rigidity of number might be an inadequate tool to address this question in the first place, as everything “characteristically fluctuating and indefinite,” for example raindrops, stands “in strong contrast to the definiteness and fixity of the concepts and objects of mathematics” (xvii–xviii). Nonetheless, Xanther surprises the reader with creative and highly interesting ideas, imagining situations in which she “froze it all, suspended the whole storm with a wish” or ameliorating her situation by “flipping the horizon” and consulting a waterproof “computer” which could be helpful in determining “the average between where drops start and where drops finish” (TFv1 60-61).
Staggering Numbers
Xanther’s questions regarding the physics and metaphysics of numbers will now be brought together with the previous discussion on the voluminousness and heaviness of The Familiar, resulting in a streak of staggering numbers that primarily concerns the Ibrahim family. While, as we have seen, Xanther deals with “one million Hows, two million Wheres, and seven million Whys!” (TFv1 57), Anwar is confronted, as soon as the second page of his first chapter, with family finances regarding the “$20,000” that Xanther’s dog will cost:
Due to the proximity of the two chapters, these numerical insertions can be viewed in parallel: Xanther engages in a metaphysical arithmetic to determine the number of raindrops, whereas Anwar is engaged in the concrete and real numbers regarding the bookkeeping of his family, taking stock of income and expenditure. Regarding their financial situation, it is clear that Xanther’s surprise will leave a sizeable dent in their bank account, so that, understandably, the “number still staggers Anwar [staggers Astair as well]” (TFv1 84). Here, the numerical aesthetic discloses that Xanther’s compulsive counting is too metaphysically complicated to be resolved satisfactorily, whereas the financial numbers are always all too clear for Anwar and Astair: their numbers have a stone-cold determinacy. In other words, while the count of raindrops is never explicitly given as a number, the financial numbers constantly recur in the Ibrahim story arc, as they are made visible to the reader via the many increments of $9,000 ($18,000) Anwar earns through his services for Enzio by debugging Cataplyst-1 and -2 (TFv2 109, 687; TFv3 165) and the losses they suffer through Xiomara’s breaking of the valuable glass wolves “Lares & Penates” worth $85,000 (TFv3 126) and Xanther’s cutting her $5,000 Saint Laurent coat (TFv4 191), which could even peak at $7,200 (TFv4 111), to not disturb her cat sleeping on it. Therefore, both Xanther and Anwar deal with staggering numbers, but they pertain to radically different domains.
As the Ibrahims are plagued by such staggering numbers, so are they overwhelmed with numbers from another source: information technology. Astair reproduces Anwar’s term when she finds “the number of missed calls staggering (Astair can’t face the number)” (TFv1 119, my emphasis). Of course, this refers to Mefisto Dazine’s ominous “prank”: Mefisto, with intentions we never learn about, has divulged to an advertisement company their phone numbers, email addresses, and other contact information, making the Ibrahims the target of an insidious and unrelentless spam campaign. The escalating intensity of the rain is thus paralleled by the numerical intensification of the spam attack. When Anwar is interrupted by a spam message, he “fails to resist now peeking at his phone,” seeing the following worrisome statistics:
| Voice Mail: | Full | |
| Missed Calls: | 117 | |
| Text Messages: | 2187 | (TFv1 88) |
A few hours later—and it is important to stress that it is in fact only a few hours, between 08:43 and 13:47 to be exact—Anwar again “does make the mistake of looking at his phone:”
| Voice Mail: | Full | |
| Missed Calls: | 314 | |
| Text Messages: | 6999 | (TFv1 376) |
Furthermore, Anwar registers the number “[r]egarding e-mails: 30.653 spam messages alone!” (TFv1 376), and the first reaction Taymor has when “Astair holds up her phone (iMessages 13.932 (is that possible?)) is that “[t]he numbers stupefy her friend (they should stupefy Astair)” (TFv1 263). Thus, from three distinct areas, we find in the first chapters of the first volume of The Familiar the Ibrahims haunted by the specter of the staggering number via raindrops, money, and communication.
Even though the Danielewskian triad of raindrops, money, and communication is predominantly conveyed with a strong numerical undercurrent, a comparison relating to the emotional response triggered by these numbers yields further familiarities between Anwar and Xanther. Coincidentally, Anwar “feed[s] the pain” (TFv1 88) the first time he reluctantly dares cast a glance at his phone, and he senses “his headache returning” (TFv1 376) at the second involuntary peek that shows how the spamming attack has amplified. Although the wording is not reproduced verbatim, these two sentiments relating to the headache are also Xanther’s when counting the raindrops. Also, Xanther tries to resist the numerical barrage like Anwar resists looking at his phone, but both eventually yield to its pull. In fact, upon a closer look The Familiar is teeming with a conceptual superposition between “rain” and “computer information,” evident in phrases such as “Anwar’s e-mail accounts all suffering the deluge too” (TFv1 119), “sea of data” (TFv1 149), “torrent of unwanted calls and e-mails” (TFv1 350), and “[f]lood the phone” (TFv4 473). Furthermore, when Xanther is at Square One with Anwar, she watches code scrolling “down the screen like it was endless, maybe it was endless, and actually it did look a bit like rain” (TFv1 344). The likening of lines of code to raindrops again taps into the numerical sphere as the reader, through signiconic inclusions, joins in Anwar’s perusal of the Cataplyst source code, tracing its serial enumeration on the left-hand side. The numbers, again, are increasing over the course of the novel: Cataplyst-1 comprises at least 101,198 lines (TFv2 113), overwhelming Anwar so much that “his mind goes blank” (TFv2 114) until he is toying with the idea “to toss any and all <quantifying> integers out the window” (TFv2 120). It also is hardly surprising that during his visit, Mefisto has modified Anwar’s game engine M.E.T. so much that “it is worthy […] renaming it M.E.T.E.,” considering “how much Mefisto has added” (TFv4 106), namely “[o]ver a million lines. Easily” (TFv3 693), or rather “millions of lines” (TFv4 106). Both Anwar and Xanther are similarly overwhelmed by the sudden surge in their respective objects of interest—raindrops and lines of code looking like rain—aesthetically captured by the numerical crescendo, which becomes even more impactful and visceral to the reader through Danielewski’s signiconicism. With a view to further conceptualizing this sense of overwhelmingness conveyed through signiconic elements, the following will introduce the sublime through the aesthetic theory of Kant.
The Signiconic Sublime
On the basis of the preceding discussion on staggering numbers, I will now describe how Danielewski uses both numerical and topological conceits at the same time to invoke two slightly different senses of being overwhelmed: metaphysically and physically. For this purpose, it is crucial to consider Danielewski’s coinage of a new genre, the signiconic, which points to a reduction of text so as to clear the space necessary for a new mode of perception; in his words, the “[s]igniconic = sign + icon. Rather than engage those textual faculties of the mind remediating the pictorial or those visual faculties remediating language, the signiconic simultaneously engages both in order to lessen the significance of both and therefore achieve a third perception no longer dependent on sign and image for remediating a world in which the mind plays no part” (thefamiliar.wordpress.com, 2015). In other words, a signicon is a picture drawn with linguistic signs, as opposed to strokes and lines that make up a conventional image: thus, a signicon can be read like a text and beheld like a portrait interchangeably, and either combination of those constitutes what Danielewski calls a “third perception.” In order to understand in how far these senses of being overwhelmed are invoked, it is important to stress that the signiconic is a spectrum that has “reading” and “beholding” as its extremes, with the former connoting a more cognitive, and the latter a more aesthetic apperception.
In the present case of the rain images, the linguistic signs with which Danielewski draws the raindrops are letters that make up entire phrases and questions, most notably “How many raindrops?” This feeling of being overwhelmed emerges through a crescendo of raindrops that unloads in massive discrete chunks after short time intervals. In other words, although we do not see the rain surging in real time, we witness in awe how quickly the rain has accumulated an enormous intensity through signiconic snapshots. In this way, Danielewski compensates the lack of dynamic movement a novel is unable to offer with a poetics of number, as he correlates the purely qualitative phenomenon of “rain” on a spectrum between a drizzle and a cloudburst with a quantitative dimension of “number” that ranges from single raindrops to a multitude. For example, Xanther’s first chapter only spans a little more than 16 minutes, but the proliferation of one raindrop (TFv1 49) to three (TFv1 51) to tens (TFv1 61-62) to several hundreds (TFv1 64-65; 68-69) is so captivating that it feels significantly longer.
However, as the raindrops proliferate, we witness that the linguistic dimension gradually gives way to a more aesthetic or dynamic depiction of the rainstorm. Especially when Xanther rescues Redwood from the drain, a different aesthetics of the signiconic comes to the fore: with multiple shades of grey and mirrored letters and signs written on top of other signs, the phrase “How many raindrops?” is only barely legible (TFv1 478-79; 494-04; 506-07), and later rendered completely undecipherable (TFv1 514-15). This not only shifts balance from the textual to the pictorial but also from principally countable raindrops to an uncountable blob or smearing, which will become a central motif in the later discussion of Xanther’s epilepsy.
This conceit informs us about the unique aesthetics of the signiconic as it invokes a specific register of the sublime. As we find here an interface between raindrops and countability, it is useful to recall Kant’s terminology of the sublime precisely because the Critique of Judgment (1790) distinguishes between a mathematical and a dynamic form of the sublime. According to Kant’s definition, “the sublime” is “that which is absolutely great” (131), and this greatness may phenomenally appear as something great in size or number, such as the Grand Canyon, a mountain, or the stars, which Kant calls the mathematically sublime. It may also appear as something great in intensity or force, such as “threatening cliffs, thundering clouds […], a lofty waterfall, etc.,” all of which “make our capacity to resist into an insignificant trifle in comparison with their power” (144), which he calls the dynamically sublime. In order to judge the greatness of any object, we rely on two modes of apperception: “The estimation of magnitude by means of numerical concepts (or their signs in algebra) is mathematical, but that in mere intuition (measured by eye) is aesthetic” (134). Note that Kant’s distinction echoes the preceding discussion on how the signiconic alternates between a more cognitive and a more aesthetic reception.
Based on Kant’s terminology, we may now articulate the unique way Danielewski’s signiconicism invokes the sublime: when we view the dynamically sublime rainstorm, our judgment is predicated on a combination of both the mathematical and aesthetic “estimation of magnitude,” that is, it is judged both “by means of numerical concepts” as well as “by eye.” First, let me clarify what in the context of the signiconic is meant by estimating magnitudes “intuitively” or “by eye.” For this, the concept of subitizing is helpful, a concept that Anwar teaches Xanther during their layover at Square One: “Subitize […] means to quantify without counting. So when you see a 5 or a 6 on the side of a dice you don’t count the five or six dots individually but know at once the number” (TFv1 346). The reader subitizes in the same way when they glance at a single raindrop (TFv1 49) or at three raindrops (TFv1 51; 55), being able to determine the number without engaging in conscious counting. Subitizing is thus a method of quantifying “intuitively”7 as it bypasses the necessity of a cognitive engagement. As the number of raindrops grows, it becomes increasingly difficult to rely on such intuition, and a closer and a more long-lasting inspection with shifting attention would instead be required: this is the psychological definition of counting, a mathematical determination of magnitude. It is precisely this transition from the subitizing range, in which quantifying is easily manageable, to the staggering range, in which quantifying would be a daunting endeavor, that introduces the mathematically sublime,8 overpowering the faculty of imagination.
Let me clarify what is meant by such an overpowering of imagination. For this purpose, Kant introduces the two terms “apprehension” and “comprehension”:
To take up a quantum in the imagination intuitively, in order to be able to use it as a measure or a unit for the estimation of magnitude by means of numbers, involves two actions of this faculty: apprehension (apprehensio) and comprehension (comprehensio aesthetica). There is no difficulty with apprehension, because it can go on to infinity; but comprehension becomes ever more difficult the further apprehension advances, and soon reaches its maximum, namely the aesthetically greatest basic measure for the estimation of magnitude. (135)
Thus, to apprehend means to progressively add up the basic units (raindrops) of a given object (rain), which could theoretically be continued to infinity; however, the more one apprehends, the more difficult it is to intuit, or comprehend, the entire object. When counting raindrops, this phenomenon reveals itself whenever one loses track of which raindrops have already been counted and which are still left for apprehension. Consequently, Kant locates the mathematically sublime at the moment “our imagination, even in its greatest effort with regard to the comprehension of a given object in a whole of intuition (hence for the presentation of the idea of reason) that is demanded for it, demonstrates its limits and inadequacy” (139-40). Therefore, the feeling of the mathematically sublime emerges whenever there is a disconnect between our proclivity and capacity to intuit the dimensions of a given object. In this specific case, such an intuition or immediate comprehension is tantamount to subitizing, while apprehension without comprehension results in a feeling of overwhelmingness, an impotence of the imagination, that cannot at once produce the whole of a given object.
Later, however, during Xanther’s rescue mission of Redwood, Danielewski’s signicons of rain depict a principally uncountable rain, invoking a slightly different register of the sublime. Using Kant’s terminology, this transition from “countable raindrops” to “uncountable rain” can be explained as a transition from the mathematically to the dynamically sublime. As we have seen, the mathematically sublime is introduced through questions such as “How many raindrops?” amidst other equally difficult metaphysical questions, all of which emphasize that any adequate response to that question would be colossal. In the dynamically sublime, on the other hand, the question “How many raindrops?” fades into the background, and the depiction of force and velocity is more pronounced; thus, the dynamically sublime is more connoted with what can overpower all physical resistance as opposed to the rational apparatus that measures mathematically, analogous to how Kant distinguishes between the two as outlined above. This is also the rain Xanther is exposed to, as “she’s outracing questions” (TFv1 480), and the rain indeed makes Xanther trip over and fall multiple times: “The rain falls so hard it seems to leap up from the street, chest high, eyes high, hovering between gravities” (TFv1 480). In other words, as the text becomes muddier and more illegible, a form of sublime dynamicism enters the signiconic, replacing the metaphysical aspect of counting. This mirrors the plot in crucial ways: the mathematically sublime captures Xanther’s feeling of being overwhelmed by the myriad of questions reified as raindrops while she was safely positioned in the car; the dynamically sublime captures the overwhelming power of the rainstorm as she is directly exposed to it.
In addition to these considerations, we can also adopt Kant’s aesthetic theory once more for the purpose of explaining how this dynamicism is tied to uncountability. Since the raindrops have become muddier partly as a result of being clumped together, we refrain from apprehending or counting raindrops altogether, which gives way to a more comprehensive perception of the totality of rain. In other words, it is more a macroscopic zooming out than a microscopic zooming in. This also invokes the register of simultaneity of all raindrops, which gives a more panoramic and violent depiction of the rainstorm. This simultaneity is only possible because it dispenses with one requirement of all acts of apprehension, namely a time-consuming “movement” of the imagination:
The measurement of a space (as apprehension) is at the same time the description of it, thus an objective movement in the imagination and a progression; by contrast, the comprehension of multiplicity in the unity not of thought but of intuition, hence the comprehension in one moment of that which is successively apprehended, is a regression, which in turn cancels the time-condition in the progression of the imagination and makes simultaneity intuitable. (142)
Thus, serial apprehension or counting cannot be achieved without such a “movement in the imagination” that results in a delay, but in all acts of comprehension such a delay or “time-condition” is suspended and thus simultaneous. This explains how the quantity of raindrops, a colossal number that invokes the mathematically sublime, is superseded by the quality of rain, a power of nature that invokes the dynamically sublime; while the former is apprehended serially, the latter is comprehended simultaneously.
Let me offer one final example of the signiconic that invokes a similar aesthetics of the dynamically sublime, this time regarding the torrent of incoming messages on mobile devices. When Xanther is in New York with Anwar to meet Myla, an acquaintance of Anwar’s, and Nathan Muellenson, a functionary of Galvadyne, Inc., she texts Astair to ensure the well-being of her cat:
Xanther sends even more messages, wherefore the abbreviated quote presented here cannot do justice to the actual flooding of Astair’s phone, which, the comedy of the scene notwithstanding, is disturbing. Here it becomes once more evident that the real-time unspooling is suspended only to gush forth in an outbreak of simultaneity with drastic consequences: its discharge is overwhelming and obstructive, almost like the bursting of an aneurysm. Astair is sure that the texts have been “delayed” and cannot be apprehended serially but must be comprehended simultaneously. This is how the concept of messaging assumes the traits of a “flood.” Xanther herself articulates this point in a meeting with Dr. Potts, referring to the spam attack her parents have suffered: “Yesterday I tried to tell Mom how all these calls are kinda like an attack. You know like so much coming in you’re paralyzed? Except at home the lights stay on” (TFv1 192). This remark not only captures the feeling of overwhelmingness this section was dedicated to, but it also opens the gateway to the following analysis, in which I argue that the numerical dimension in The Familiar is related in many ways to Xanther’s epilepsy.
Xanther’s Epilepsy: Dov and Numbers
A crucial insight given by Xanther herself establishes a link between information overload and her epileptic attacks, as “sometimes people describe seizures as an overwhelming amount of information in the brain” (TFv1 350). Given her perpetual confrontation with staggering numbers like those previously mentioned, Xanther is constantly liable to yet another fit. Regardless, Xanther adamantly confronts the task of counting raindrops, or counting in general, which can be explained by examining her relationship with Dov Z. Mudd, her biological father.
The only feasible way to count raindrops—a highly dangerous undertaking for her, because she might suffer a seizure in the process—is to somehow suspend their fall onto the ground, so that she might count “every drop with a finger” (TFv1 63). In Xanther’s perception, the fall of the raindrops is reminiscent of a “flickering,” a well-known trigger of epileptic attacks in photosensitive patients. Xanther excels in her courage to entertain the idea that a conclusive count of the raindrops might ameliorate her situation; this is why she is intrigued at Square One, when a glitch freezes the game, seeing in “frozen red droplets” another version of “frozen rain,” which she bets “uhm, like right?, you could count every single drop?” (TFv1 348). Anwar’s colleague Glasgow, much like the reader at this point, in turn wonders: “Count them? […] Sure. But why would you want to?” (TFv1 348)
It is indeed a fundamental question: why would Xanther want to freeze the rain and count each raindrop? An underlying rationale behind counting is related to the concept of identification and naming and an introduction of order into chaos. As David Berlinski notes in One, Two, Three:
A counting endows things with their identity, so it imposes on them their difference. Three sheep make for three things. The natural numbers are the expression in nature of division and distinctness. Between the number one and the number two there is, after all, nothing whatsoever, and nothing between things that are distinct either, however much alike they might be in various respects. The discreteness of the natural numbers is as absolute as the one enforced by the surface of our skin, which permits contact but not, alas, commingling. (8)
Hence, the underlying logic of counting is that it emblazons each object with a number, thus also demarcating its boundaries. Stewart Shapiro puts it succinctly when he likens counting to naming by drawing on Frege’s philosophy of arithmetic: “As Frege intends it, the phrase ‘the number of F’ is a grammatical form for denoting an object. That is, ‘the number of F’ is a proper name (broadly speaking)” (110). The problem that quickly arises for Xanther is that the naming process is only applicable during the transition phase of falling, because raindrops commingle upon their “impact,” so that “rain becomes meat” resembling “meatish meatless shapes” (TFv1 62). This phenomenon is also addressed in Andrei Tarkovsky’s 1983 film Nostalghia, featuring a mathematician who is utterly devastated by the fact that he cannot reconcile the mathematical truism of “1 + 1 = 2” with the raindrop phenomenology of “1 + 1 = 1.” We will see later that the formula “1 + 1 = 1” will be crucial in evaluating the symbiosis between Xanther and Redwood, her cat, and the fact that their symbiosis cannot be “counted” and adequately tagged with numbers bespeaks the general shortcoming of the numerical to address the convoluted and entangled.
Indeed, there seems to be an impasse in numbers to address mixed and not clearly demarcated phenomena. Berlinski mentions this impasse in counting as well: “There are certainly substances in the world that cannot be counted—mud, for example. The word ‘mud’ seems indifferently to designate mud wherever it is and however it may be found” (8). This is also expressed in Thomas Pynchon’s novel Mason & Dixon (1997), in which astronomer Charles Mason understands that “Stars and Mud, ever conjugate, a Paradox to consider” (724), as “Stars” embody mathematically regulated, countable objects, and “Mud” embodies the antithesis of such a regulation. In The Familiar, mud also paradigmatically refers to a chaotic mixture, an uncountable, disorderly smear that defies all differentiation.
However, “mud” also evokes Xanther’s biological father Dov Z. Mudd, memories of whom are constantly interspersed into the Ibrahim narrative arc. A particular memory, namely Dov taking Xanther to “Hyperion,” a major Los Angeles sewage treatment plant, is conducive to understanding why Xanther is so bent on counting raindrops. Dov is depicted as an overprotective father, who constantly drills Xanther to be “not afraid […]. Stare a thing in the eye. Know it. And let it know you know it too before you let it go. You’re a Mudd. Don’t forget” (TFv3 519). Before the gigantic “screens” that display an extremely nauseating mixture of “rags, tampons, plastic wrapping, and […] slats of slanted metal drooling brown refuse” (TFv3 517), Dov uses the occasion for a lesson: “So I brought you here this morning to show you unity, oneness. […] That’s right, kiddo. This. Not so pretty, huh? This is a world without boundaries. This is what happens when there are no divisions. Look at it Xanther, breathe it in, never forget: this is what you get when there is no law. This is what you get when the teeth lose” (TFv3 521). This traumatic event has imprinted itself on Xanther’s memory, which becomes evident when she, observing an ant colony, ponders “grinding them up with her teeth” (TFv3 522) to ascertain their crushing power. These examples show why Xanther feels immediately uncomfortable in situations she cannot order by counting, as it is predominantly a “muddiness,” a lack of shape that numbers cannot adequately differentiate.
Xanther’s epilepsy points to yet another aspect, namely an internalized and constantly ignited conflict due to Dov’s contradictory teaching, and I argue that this contradiction becomes manifest in the epileptic shaking and tremor. In Hyperion, Dov teaches Xanther that a world without boundaries is a world replete with “disease, destitution, and delusion, and a total disregard for the individual” (TFv3 521), but at the same time, and herein lies the contradiction, he urges Xanther to embrace being a Mudd, or mud, and in fact to be “tougher than mud. Don’t forget it. Love, Dov” (TFv1 129). As Astair explains, this is because “[m]ud (to Dov’s mind (aside from being his patronymic)) was beyond defeat. Boot heels, bullets, and tanks could tear it up and mud would be none the worse. Sometimes Dov even hinted that death itself had nothing on mud” (TFv3 129).9 Xanther’s desperation springs from this simultaneous glorification and denouncement of mud, and it becomes evident with regards to a metaphor she chooses for her mental state: upon Anwar’s failed explanation of why a game engine is called “engine” in the first place, Xanther reports that the explanation “had seemed to make it clearer for a moment. And then everything got muddier again, even if mud was one of the goals, lots of mud, African mud, Asian mud, all kinds of muddy places with wild animals and predators ‘of all sorts’” (TFv1 329). The muddiness of her thoughts is synonymous with helplessness, yet it is also “one of the goals”; here, the reader understands before Xanther that she is caught in a quagmire. According to Dov’s logic, mud is indeed unconquerable and indestructible, but it comes at a price of sacrificing the aspects of individuality according to Dov’s own allegory during their visit to Hyperion.
With all this in mind, it does make sense that, during her Question Game in the rainstorm, Xanther responds to Anwar that she is thinking about “Dov” (TFv1 72). First of all, the reader may be prompted to suspect that Xanther is lying in that particular situation, even though she repeatedly confesses how much she hates it. When the reader later learns who Dov is, and also how much Xanther still suffers from his premature death only a few months ago, the reader believes that Xanther wants to deflect the topic of epilepsy under the pretext of mourning Dov. In fact, she even admits to Dr. Potts she does not want to worry her parents regarding her illness because they do “so much for [her] already” (TFv1 191). Also, the reader spots, amidst the falling raindrops, sentences such as “Xanther’s the zero” and “Xanther’s the drain” (TFv1 69), showing that she wholly takes on the double culpability not only for her sickness, but also for the economic burden on her parents.10 However, on a deeper, unconscious level, she might be telling the truth about thinking of Dov while watching the rain. Through three layers of smearing, with her “entoptic” ocular condition of seeing “floaters” (TFv1 227) and with her glasses “all fogged up, lenses now just smudged” and “way damp,” and the raindrops losing their form and puddling against the wind shield, she recognizes the “world is a smear, even with wipers on high, how she feels feels all smeary too, are there wipers for that?” (TFv1 463). She might be thinking of Dov here because the ubiquitous smearing is reminiscent of her Hyperion experience. Due to the contradiction in Dov’s worldview, it is understandable that she imagines a scenario of frozen rain, because that would sustain the proper boundaries of all objects and inhibit the smearing so she could tag them with numbers. Counting, thus, would constitute an act of naming that would, in turn, counteract the Hyperion-esque smearing of the world; as she tells Dr. Potts, “for some reason naming is a big thing for Xanther, because, like, they promise to keep things still or at least steadier, like numbers in a way” (TFv1 188). However, contrary to her phantasma of frozen rain, there is another drive operative in Xanther that wants to annihilate all boundaries, and that conflict is a sublimated conflict of Dov’s contradictory influence. As she watches a little ant colony marching through her house, Xanther is
caressing each little insect with a specificity all its own, an individuality to tend and clean as carefully as each tiny antenna, and all Xanther would have to do is open her mouth and set them free. Imagine that! A name for every ant, hundreds too!, […] What stops that pronouncement isn’t Anwar’s arrival but an equally sudden impulse to crush them all too, appalling Xanther with the sudden rush, to make a nameless smear out of this intrusion, which sickens her as well as tingles her lips with shame, drool starting to lay siege to the corner of her lips, all she cannot swallow. (TFv3 382)
The marching of the ant colony is parallelized to the falling of the raindrops. Xanther is thus positioned right between the urge to keep the world rigid and fluid at the same time, and that imbalance is largely a product of Dov’s paradox.
The epileptic moment for Xanther, then, can be regarded as the state of a convulsive oscillation between these two states of rigidity and fluidity, between the countable objects and the uncountable smear, between raindrops and rain. Danielewski articulates the tension of this aesthetic correspondence in two ways: with aesthetically powerful and poignant signiconic manipulations, which I have already hinted at through the discussions on the mathematically and dynamically sublime, and by describing Xanther’s bodily state after a seizure. In the first season, Xanther has her most severe epileptic fit during the inaugural performance of Myla’s ballet Hades. The portents are clear right away: she is “shaking all over” like she is “at the start of every seizure” (TFv4 524). The following pages depict, again with swelling intensity as previously mentioned, how droplets overlay and distort the text, many of which burst upon impact like raindrops on the ground, ultimately rendering the text entirely illegible. Of course, the bursting of the bubble is precisely the threshold between form and chaos, between contour and smear, which Xanther’s phantasma of frozen rain aims at maintaining. Furthermore, Xanther’s outward appearance after her seizure shows that the egress of body fluids is a phenomenological aftereffect of epilepsy: “Ruptured cuticles. Contusions on her arms. […] A tongue bruised so badly it was black as a cobra. Xanther’s eyes had seemed inked in blood” (TFv4 695). The emotional grip these pages exert upon the reader is also largely due to the synchronization between the aesthetic makeup of the pages and the mise-en-scène in the play Hades, which oscillates between the orderly and countable caging of the demons in Hades’s “centrifugal” pirouette and the disorderly and uncountable release of the demons during Hades’s “centripetal” pirouette.
As it also once happened to Xanther, in response to Satya’s release from her cage, that she had wet herself, sensing “the growing puddle around her feet” (TFv3 805), Redwood is disproportionately more threatened to “dissolve.” Both seem to be somewhat entangled, or “entwined” to use the wording of the Venice witch during the final Entra’acte (TFv5 833), which becomes most prominent when they both experience the Hades seizure even across the distance between Los Angeles and New York. The fact that Redwood might suffer seizures in the future was somewhat hinted at in the beginning, as it became habitual for Xanther to clean her cat’s eyes of mucus. In the fifth volume Redwood, however, the epileptic smearing is aggravated and reaches its climax: “The sweater grows damp (is It also urinating? (of course it is)). Xanther unwraps the trembling rigidity to reveal (instead of (in addition to?) urine) a (clear) mucus egressing from its anus. A moment later equally clear (viscous) fluids start to leak from its shuddering mouth […]” (TFv5 67).
To complement this phenomenology of epilepsy, it is worth noting that the aesthetic register of this smearing is reminiscent of two short stories by Edgar Allan Poe, namely “The Facts in the Case of M. Valdemar” (1845) and “Berenice” (1835). In “M. Valdemar,” a patient is arrested in hypnosis at the exact moment of death, halting his body’s decay. The corresponding tension between life and death is symbolized by “a vibratory motion […] observable in the tongue” (243) that oscillates between the “whiteness of his whiskers, in violent contrast to the blackness of his hair” (238), which allegorizes his suspension between life and death and as a motif relates to Xanther’s epileptic tremor. Furthermore, his “lowering of the pupil was accompanied by the profuse out-flowing of a yellowish ichor” (245), and shortly upon dispelling the hypnosis, his body’s rigidity collapses fast-forward into “a nearly liquid mass of loathsome—of detestable putridity” (247). Coincidentally, Xanther collecting the mucus from the cat’s eye is here reminiscent of Valdemar’s oozing from the eye. Regarding “Berenice,” the story explicitly deals with a woman who is afflicted by “a species of epilepsy not unfrequently terminating in trance—trance very nearly resembling positive dissolution” (411), and it reaches its finale when the protagonist Egaeus, himself plagued by lapses from reality, pulls out all of Berenice’s teeth in conviction that she had passed away.11 Poe’s image of the epileptic toothless body is reinvoked by the cat’s quasi-dissolution of its body when “cycling,” adumbrated by the loss of its canines: “Oh my God! What’s wrong with its mouth? Where are the front teeth? Xanther! What happened to its teeth?” (TFv5 62). Interestingly, shortly before the onset of “cycling,” Xanther had, upon jingjing’s request, engaged in counting its teeth (“Fine! Fine! I’m counting” (TFv5 60)) with a view to confirm its identity, which again contrasts form and smear through the aspect of countability.
Thus, the resurfacing of Dov’s memories in Xanther attests to a psychological undercurrent in the epileptic shaking and vibrating between life and death, with death understood here as the constant threat of the disorderly smearing of life. This resonates with Jeanette Stirling’s work on the iconography of epilepsy in her book Representing Epilepsy, in which she argues that “as a figurative device, ‘the epileptic’ is inevitably poised on an unstable threshold between order and an ever-threatening chaos” (xv). As for Redwood, the reference to Erwin Schrödinger is crucial. Schrödinger has arguably become most famous for his thought experiment of “Schrödinger’s cat,” which illustrates the ontological and epistemological consequences of quantum mechanics. In that thought experiment, a cat is ensconced in a hermetically sealed box and connected to an apparatus that would kill the cat if a random event, such as the decay of a radioactive substance, occurs. Up until the moment the box is opened so as to confirm or deny the death of the cat, it is surmised to be both dead and alive at the same time. Interestingly, Schrödinger’s own wording is suggestive of Danielewski’s aesthetic register, because, prior to an act of measurement, we would assume that “in it the living and the dead cat (pardon the expression) mixed or smeared [verschmiert] out in equal parts” (328). Although it was always suggested that the cat exists in a mysterious limbo between being young and old12 and also between being alive and dead, because the “ID came back as deceased” (TFv2 104), it is only during the exacerbation of its epilepsy, its “cycling,” that the Schrödinger-esque smearing commences. The quantum-theoretical dimension of the epileptic is then rearticulated by Anwar, who must watch, during the performance of Hades, his “dear child still seized in that peculiar battle between rigidity and fluidity {the domination of one superimposed over the other <only to submit «with the next twitch ☾and twist☽» to the other’s primacy” (TFv5 57). Here, the quantum-theoretical marker is the word “superimposed,” which designates the adding together of quantum states into a new state in a process labelled “quantum superposition.” Danielewski’s multiple references to quantum theory not only invoke the “smearing” of Schrödinger’s cat, which taps into the register of epileptic smearing, but they also provoke the hypothesis that Xanther and Redwood are somewhat “entangled.” Therefore, their symbiosis evades the parameters of classical Newtonian physics and may only be assessed from a more “complicated” vantage that does not permit a conventional arithmetization, for which Danielewski will reserve the paradoxical equation 1 = 2, as we shall see shortly.
Smearing versus Shearing
I have previously argued that the “muddiness” of the world defies numerical signification, which makes Xanther feel uneasy. Now, establishing a reference to an episode in Anwar’s past in Cairo that constantly haunts him like Dov haunts Xanther, I want to illustrate how this epileptic smearing defies the number from another angle. During the expansion of the shockwave in the Ibrahim’s living room, Anwar remembers the trauma of 1984, in which purportedly an “Israeli bomb” (TFv5 736) destroyed his house in Cairo, killing Fatima and Shenouda, his parents. The imagery surrounding Anwar’s remembering is revealing, especially the picture of shattered glass that introduces the chapter. Shattered glass not only harks back to the broken porcelain from three hours ago, when Anwar was filled with indignation to see Jingjing attack Xanther, with “the tray long gone from Anwar’s hands // all cups // silverware too // the teapot // every comestible // tumbling // down through the air” (TFv5 374-75), but it also activates precisely that traumatic memory of the bomb in Cairo, which also featured “shattering glass” that “keeps shattering in some awful loop” (TFv5 732-33). Anwar’s memory of the aftermath of the explosion also features a mysterious “tiny white cat” which “had sat for hours on one I-beam between where there was no more ceiling and no more floor” (TFv5 738). Considering that Xanther’s cat seemingly traveled the distance between Singapore and Los Angeles with ease somehow, this raises the question whether the cats from Anwar’s past and Xanther’s are in fact identical.
What is more, Anwar ruminates on a mathematical function, namely “Arnold’s cat map,” whose namesake is the Russian mathematician V. I. Arnold (TFv5 739):
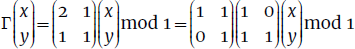
Befitting a math-savvy software developer, Anwar captures almost the entirety of his trauma with this function and its highly intriguing and surprising characteristics. Before we can get to the traumatic aspect, we must elucidate the mechanisms behind Arnold’s cat map. One can imagine the map operating on a square, for instance a photograph, by pushing the image on the square one unit into the horizontal direction and two units into the vertical direction, twisting it slightly, which is referred to as shearing in mathematics. Then, the modulo operator is performed on the larger image, which slices up the sheared image and squeezes the slices back into the original square. The image is called “Arnold’s cat map” because Arnold’s illustrations of the map were exemplified with the photograph of a cat. Taking to heart Anwar’s realization that “[i]mage subitizes language” (TFv1 346), Arnold’s own depiction in Ergodic Problems of Classical Mechanics (5–6) presents its mechanisms constructively:
The bottom-left tile shows the original image of the cat on which the map operates by shearing it into the larger, slightly bent cat. The bottom-right tile shows the “reassembled” cat after the modulo operation is performed on the sheared cat. The individual slices of this reassembled cat are composed of the triangular pieces of the sheared cat in the upper tiles. To verify this, one can imagine cutting along the vertical and horizontal grid of the tiles and then cut the pieces of the sheared cat out of the tiles. This produces four triangular “shards,” which one can, like a jigsaw puzzle, reassemble into a single tile, obtaining the bottom right picture as a result.
The remarkable properties of Arnold’s cat map are revealed by repeating this process numerous times. The image in the bottom-right tile shows the first iteration after shearing, cutting, and reassembling the original cat. The same process will now, in a second iteration, be applied to the disfigured cat from the previous process. That yields a far more chaotic and fragmented picture, which Arnold also presents in the lowest tile. After the first iteration, one could still hypothesize that the shards are indeed remnants from the picture of a cat, but the second iteration already is too deformed to suggest any similitude. What is striking, however, is that the image of the original cat will recur after a sufficiently large number of iterations.13 This is striking because it goes against our instincts pertaining to entropy, in the sense that additional chaotic mixing of the sheared pieces of the cat should never reconfigure the original cat again.
Reapplying these insights to Anwar, Arnold’s cat map offers an evocative depiction of how paranoia and traumatic flashbacks affect his psychology. Not only does the reference convey the uncanny idea that the white cat in Anwar’s house in Cairo has been shredded to pieces by the blast and mysteriously reassembled itself, but also how old configurations always recur or, to use a gorier terminology, how Anwar re-members the dis-membered. Danielewski transports this onto yet another level by interlocking Anwar’s trauma with the idea of a graphics engine, which similarly slices reality into polygons and puts them together. That is the dominant aesthetics described in the entire Square One get-together, as Glasgow reports that “spraying blood is just geometry” or “animals look like polygons” (TFv1 349), which makes Xanther think about the “frozen rain” idea in the first place. Danielewski thus endows Anwar’s statement “[b]ombs are never neat [{one square makes two triangles…} they make shards…] (TFv2 123) with a double hermeneutic capacity, insofar as it correlates his profession as a graphics designer, who reassembles the “shards” on the computer screen to produce images, with his bombing trauma, emblematized by the white cat, that constantly reassembles itself and “keeps shattering in some awful loop” (TFv5 733).
This little excursus into the mind of Anwar conjures an important distinction between the epileptic and the computational. Danielewski strongly connotes the epileptic moment with an aesthetics of smearing, in contrast to connoting the computational moment with an aesthetics of shearing. As smearing resists counting by overflowing all contours, shearing introduces a polygonization that is mixing while retaining contours. Note also that in The Tree of Knowledge by the biologists Humberto Maturana and Francisco Varela, epilepsy is described as a “neurologic syndrome which, at its worst, produces centers that generate waves of electrical activity. These waves spread over the cortex without regulation” (225)—again a metaphor of an uncontrollable overflowing without any safeguarding boundaries. On the other hand, in the illustration of Arnold’s cat map provided above, one can spot even in the second iteration the rigid contours of the shards that are put in place. Also, as Anwar points out, one “might say these graphics represent, in a way that’s instantly quantifiable, the parametrics of the code” (TFv1 345), whereas the epileptic moment obfuscates the process of quantification. Anwar’s thought processes and imaginations are so heavily infused with a coding grammar found in programming languages such as C++ that he quite literally thinks in code, not least suggested by the many parentheses that dominate the narrative style of his chapters. Therefore, it is not surprising to ubiquitously encounter in his imagination an aesthetics of the “shard,” as he deems the “shattering glass” (TFv5 732) to be “[w]orse than any frozen arrow,” namely a “frozen rain of glittering blades flying sideways” (TFv5 733). Furthermore, we find Anwar “in a fever trying [over and over] to reconstruct the stories of the past” by “assembling newspaper clippings” in a “collage of longing” (TFv5 734), all of which contribute to a computational aesthetics. However, Anwar’s mentioning of “frozen rain” most readily connects with Xanther’s fantasy to freeze the rain in order to count the raindrops (cf. TFv1 348), which emphasizes the discrepancy between the computational and the epileptic, the countable and the uncountable.
The Brain and the Computer
Finally, this opposition of the “shearing” and the “smearing” shows how Danielewski’s arithmopoetics introduces Xanther’s rehabilitation, as it appears in outlines that she becomes, by the end, less vulnerable to epileptic attacks. Through the entire first season, the domains of the mind or the brain have been compared to computers, especially by the contiguity between Xanther and Anwar—and in some way, the concept of the “glitch” in the code is likened to the epileptic attack as though it were a “glitch” in the brain. Such a glitch is presented in two major ways. First, both the glitch and the epileptic attack begin by an abrupt pause of movement. In the Square One episode, that is precisely the glitch that invokes the idea of “frozen rain” (TFv1 348), and during Redwood’s seizure, Astair mentions that “[i]t hardly moves” (TFv4 490). After the sudden motionlessness, the epileptic seizure induces a convulsive “shake” (cf. TFv4 499), which parallels “the spinning rainbow wheel of death” (TFv1 348) on iOS desktop computers. The second familiarity can be identified via occasional signiconic elements. The epileptic seizures are, often within a few moments before the onset, visualized by a total blackness that covers both pages in the opened book (TFv2 794-95; 798-99; 802-03; 808-09) and is thus similar to the black screen whenever Anwar encounters a malfunction in the code and the software crashes (TFv2 115-16; 121; 300-05). Of course, such a comparison between the computer and the brain has long been part of the discourse of digital information processing, evoked most notably by John von Neumann in The Computer and the Brain (1958).
Strikingly, however, Xanther at least momentarily attains an auspicious immunization against her epilepsy by incorporating an uncomputable idea, namely the arithmetic impossibility that 1 = 2, which immediately undermines the parallel just described. In order to understand this, we must consult the seven “indeterminate forms” that Anwar presents, which bracket the first volume, as they are mentioned right at the beginning (TFv1 59) and the very end (TFv1 771) of the narrative part.
These indeterminate forms, also called “⣔numeric⡲ impossibilities” (TFv1 58), have a strange effect on Xanther because one would surmise they “forest her head with questions but don’t” (TFv1 60). As Anwar shows in his calculations, the indeterminate forms are indeterminate precisely because they could yield any number depending on the context of the calculation. For instance, 0 × ∞ could in fact be calculable, however, only the context can predict if that calculation yields 0, ∞, 1, 2, or any other number whatsoever. That is why they are “indeterminate” in the first place. However, the calculation of 0/0 is of another quality, because it is truly a “fallacy” (TFv1 59). Anwar demonstrates it thus:
The 0/0 fallacy is in this regard different from the other indeterminate forms because it cannot yield a result that is consistent with the laws of mathematics.
Xanther takes great pleasure in this mathematical oddity, and she is able to “process” the repercussions of dividing by zero in a way a computer cannot. Anwar is desperate because “any error here eludes him” (TFv2 114) that constantly induces the glitching black screen, while for Xanther, the arithmetical error 1 = 2 in fact empowers her. At the end of the first season, Xanther reconsiders “Anwar’s seven indeterminate forms […] showing how dividing by zero makes a mess of math” (TFv5 214) and derives a metaphysical meaning from it:
Xanther sits up, a little stunned by the weird thought coming for her, from a completely unexpected direction too. Little on stirs with a groan.
Because if like little one her and equal one… The thought starts, but, no, that’s not it.
Because if 1 * 0 = 0 and 2 * 0 = 0 then 1 * 0 should equal 2 * 0 and does, because zero times anything is zero. The mess part comes if you try to divide both sides by zero to get rid of the zeros, that’s when you get… 1 = 2 […].
Xanther starts again.
She and little one are separate, which means, duh, like they are clearly two, unless… yes, that’s it, unless they’re divided by zero, because if they’re both divided by nothing, then their twoness can equal one. (TFv5 214)
This is Xanther’s personal way of dealing with the “mess” of “1 = 2,” reminiscent of the messy mud-and-smear aesthetics, because these “indeterminate forms” are by definition formless and defy quantification, in the sense that they preclude an unequivocal numerical result.
The equation “1 = 2” also settles the question of raindrops. Unlike the mad mathematician in Nostalghia, Xanther firmly embraces “1 = 2” as a truthful and logical proposition, or in other words, as a pacifying result that eliminates all the other metaphysical questions regarding numbers. Harking back to some of the questions the raindrops had provoked in Xanther, “1 = 2” solves the problem of 2 raindrops merging into 1 as well, along with the impossibility of counting them because they are 1 and 2 at the same time. Her technique is especially effective even in view of a more skeptical voice like Douglas Hofstadter’s, who would disqualify such an undertaking on the grounds of raindrops being too “fuzzy” to be counted in the first place: “Two raindrops running down a windowpane merge; does one plus one make one?” (56) In other words, for Xanther, “1 = 2” is a potent instrument to counter the muddiness and fuzziness of the world.
On a signiconic level, too, Xanther’s pacification of her own mind and curiosity becomes evident. At first, Xanther’s forest is depicted as a hostile, computational place. Danielewski takes it quite literally that the entire complex of counting branches off and triggers avalanches of questions, in that he visually depicts it as an arborescent and ramifying construct that “doesn’t just create one or two more questions, but, like, forests of them” (TFv1 58). That forest is depicted as cold and dangerous, picturing Xanther’s sensation of “spiky frost and needles. A real numbing has started up” (TFv1 66) whenever the questions become uncontainable. Here, Danielewski plays, on a linguistic level, with the almost homonymic relationship between “numbing” and “number.” Furthermore, the forest is replete with a computational signiconicism: the branches, resembling depictions of computation tree logic, are composed of black lines almost as thick as the glitch bars and hash keys (#), which in mathematics and programming languages is used as an operator to count (“hash”) the items in a set of data or output another number based on that set of data. Also, aggrandizing @ symbols make up the blue and red colors beneath the flicked stones, reminiscent of the @ symbol in e-mail traffic. With Xanther embracing the equation “1 = 2” and the prospective entanglement with Redwood, however, the forest transforms into a warmer and more inviting place. When she plays computer games with her friends at her place, with the cat close by, she mentions that its “just that she could also feel these moments that seemed like, well, quicker, sorta like the way she feels when she’s having these non-stop dream mash-ups, linked all over the place, branching to the nth degree of impossible, until she has to make believe they’re pine boughs, except in this case it’s like Xanther can almost keep up for an instant, and then everything gets really clear, and almost still” (TFv2 771). The stillness of her inner forest parallels the stillness or moderation in her question song, which coincides with the termination of the rain in the first volume: “Outside, the storm has passed. At least the rain has stopped. Not even branches creak anymore as they sometimes do in the aftermath of a heavy rain, when leaves and fronds now and then shift, letting go of their holdings” (TFv1 831). In other words, the parallelization of raindrops raining in Los Angeles and questions reigning in Xanther’s forest is again effective. During the first night with her new cat, “Xanther can almost hear the sky’s lifting emptiness taking away questions of numbers” (TFv1 832) with “everything in place. Arranged. Safe” (TFv1 833), and this foreshadows the image of the sky over the forest that opens up at the end of the first volume (TFv5 822-23). Equipped with “1 = 2,” Xanther is able to formulate out of the “indeterminate form” a unification with her cat that induces a surge of empowerment, as “everything suddenly feels manageable. Or better: answerable” (TFv1 837-39). Therefore, Danielewski installs “1 = 2”—or, in a slightly altered form, “1 + 1 = 1”—as the “catsum” (TFv1 67) that banishes the horrors of numbers via a feline arithmetic that attains absolute truth only within the universe of The Familiar.
Mesorithmetic: Recursivity and Narcons
The third and final dimension of Danielewski’s arithmopoetics is couched between the exorithmetic and endorithmetic analyses outlined above. This is the space of resonances between form and content, between format and substance. Repeating the terminology alone is already somehow eerily reminiscent of the different numerical conceits negotiated in the diegetic world of The Familiar itself. By freezing the rain, Xanther fantasizes about immortalizing “form,”, just like Danielewski uses arithmetical constraints (9, 27, 30, 880) to keep in check a narrative replete with many individual strains and prevent it from becoming ever muddier. In some sense, a single numbered volume of The Familiar could be to the entire series like a raindrop is to rain.
I have already touched on the importance of the number 27 that denotes the contingent of The Familiar. That exact number, however, recurs obliquely in the diegetic world (TFv1 180). As 27 is a cubic number, we could transfer that knowledge onto an object Xanther fiddles with in her therapy sessions with Dr. Potts: a Rubik’s Cube. Such an object is composed of exactly 27 minor cubes, which invites a comparison between its mechanism and the mechanism of the serial novel at large. We find on each of the 6 sides of a Rubik’s Cube an immovable cube at the center that carries the color of the plane and each act of the novel is similarly composed of 6 colors that occupy the centers of the act with various other characters going in on out of the plane. Furthermore, the cuboid geometry of the Rubik’s Cube underscores the aspect of “voluminousness” as previously outlined.
The dimensions of the Rubik’s Cube also point to another arc of recursion in the novel pertaining to Xanther’s epileptic seizure, when Dov died on 23rd of December, 2013. The seizure she suffers is classified as a “convulsive status epilepticus” (TFv1 245) and is, as such, by far “the longest. Ever” (TFv1 253), at 5 minutes and 33 seconds (TFv1 254). A conversion of that time to seconds yields 5 × 60 + 33 = 333. Several such combinations of triplets of 3 occur on multiple levels, connecting the edge length of the Rubik’s Cube, the number of volumes in the entire series, and also Xanther’s “status epilepticus” (TFv1 245). Although Xanther’s seizure ended after 333 seconds, Danielewski’s signiconic illustrations suggest an infinite recurrence, or a recursion, by aligning the numbers from 1 to 60 in circles. During the fifth minute, the reader follows the ticking of the clock in real time, as the numbers are added incrementally, which again emphasizes the relationship of counting to Xanther’s epilepsy. Reminiscent of Anwar’s recurring trauma, Astair begins to think in the same logic of that vicious circle, as the words themselves almost form infinite loops, out of which she cannot escape:
This is one of the instances where The Familiar resonates most with the much more strict mathematical aesthetics of Only Revolutions, constituting yet another example of how arithmetic and geometry combine in Danielewski’s signiconic imagination. The arrangement of the numbers from 1 to 60 in a circle within a single image encompasses an infinity of horror and hopeless incarceration, as Xanther’s epilepsy constantly recurs. We could therefore assume that Danielewski’s circular aesthetics recurs in a different guise here; while, as previously mentioned, the numbers 36, 90, 180, and 360 were used to signify a compass of love in Only Revolutions, the number 60, regarding Xanther’s status epilepticus, signifies a vertigo of death.
Against this background, the specificity behind the numbers 9 (character count), 30 (number of chapters in a volume), and 880 (number of pages) may be emphasized, as they all relate to a cat. First, on the title page of Only Revolutions, the reader finds that it is “Volume 0: 360: ∞,” all of which are numbers that symbolize recursion, and in turn evoke Anwar’s seven “indeterminate forms” (TFv1 58) again. This prompts the hypothesis that Danielewski is playing with the zero-infinity-symbolism in his page count too, corroborated by the fact that Redwood evinces traits of an “eternally returning cat.” Therefore, one answer to our preceding arithmopoetic speculations may be one of feline arithmetic, as the page count rotated 90° anticlockwise
0
∞
∞
resembles a minimalist numerical picture of a cat, either from below or standing upright. That might also explain why each volume features 30 chapters, as cats have exactly 30 teeth, and 9 characters, as cats have 9 lives.14
Therefore, the characteristics of Redwood retroactively allow an arithmopoetic speculation as to why Danielewski might have chosen such specific numbers for his format. In addition to the feline arithmetic, the concept of recursion is featured in another instance, namely the Narcons, this time not so much in the sense of “eternal recurrence” but rather as it is used in computer science. I will offer a final arithmopoetic speculation regarding the numbers 3, 9, and 27, which denominate those Narcons featured in the first season: TF-Narcon3, TF-Narcon9, and TF-Narcon27.
The Narcons
The Familiar displays its consciousness of a narrative hierarchy and its own constructedness as narrative by introducing several types of “Narrative Construct. Narcon for short” (TFv1 565). Narcons populate an extradiegetic domain enclosing the “pure” narrative, dwelling at the threshold between the immaterial thoughts of the characters and their material enunciation on the page. Their liminality, or their residue at the threshold, is further highlighted by the fact that their intervention is not registered in the usual sense because, as their voice cannot be heard by the other characters (increasingly with the exception of Xanther), and their narrative intervention is fundamentally without number. Lacking paginations, their chapter emerges right between chapters 22 and 23. In fact, TF-Narcon9 suggests that the end of chapter 22 be a “good enough place to pause” (TFv1 564), and indeed intradiegetic time has not lapsed at all, as a quick glance on the timestamps at the end of chapter 22 (15:21:07) and beginning of chapter 23 (15:21:08) confirms. Therefore, the Narcon intervention occurs in a void of colorless whiteness, all the while unmarked by the digits of clock-time.15
The relationship between Narcons and numbers is an existential one, considering that they introduce themselves as being composed of “nothing but numbers. Zeros and ones” (TFv1 565). That is, of course, the definition of a digital machine, or a computer in the modern sense. In fact, upon a closer look, Narcons emerge as mathematical functions in the sense that a numeric or computational input yields a certain output: “For example TF-Narcon9X(Action/05102014080314081927352329728/34.0861-118.2518/xzz-xx-ghry77666/.00000000000000000000000000000000000000018749%) looks something like this:
One early Saturday morning in May, Xanther went with her
stepfather to see about a dog in Venice. It was raining hard.” (TFv1 568)
Examining the input, the argument of the function, in the preceding example gives valuable insight into the nature of the Narcons’ programming. The first word “Action” is self-explanatory; what is more obscure is the sequence of numbers after that. One might assume them to be completely random, but they are in fact not: the first eight digits, “05102014,” refer to the day, and the following 16 digits, “080314081927,” refer to the time span in which the action is performed: on 10 May 2014, between 08:03:14 and 08:19:27. After that argument slot the location is specified, as “34.0861-118.2518” indicate the latitudinal and longitudinal coordinates of Venice, Los Angeles. The percentage in the last argument slot with the long string of zeros refers to the “wide range of possible inclusions and exclusions – from 100% to ≤.00001% according to various predetermined limits” (TFv1 568), only covering a minimal fraction of what Xanther had been doing on that day. In fact, plugging in the same argument with a higher inclusion percentage would generate the first chapter of the first volume as opposed to the two lines quoted above.
The concept of recursion comes to the fore when Narcon interruptions pop up during a character’s chapter. Douglas Hofstadter’s conceptualization in Gödel, Escher, Bach (1979) proves helpful to address this topic, since he is held in high esteem for his adept navigation of fields adjacent to the brain and the computer. Hofstadter’s category of recursion is indeed “very general” and encompasses “[s]tories inside stories, movies inside movies, paintings inside paintings, Russian dolls inside Russian dolls (even parenthetical comments inside parenthetical comments!)” (127). The last statement predicts that Xanther’s parents, with their superabundance of parentheticals, elicit the concept of recursion, as do the Narcons, because they are, according to Parameter 4, “always bracketed” (TFv1 574). Hofstadter explains the recursive element in these examples by introducing three terms from computer science: push, pop, and stack: “To push means to suspend operations on the task you’re currently working on, without forgetting where you are—and to take up a new task. The new task is usually said to be ‘on a lower level’ than the earlier task. To pop is the reverse—it means to close operations on one level, and to resume operations exactly where you left off, one level higher” (128) and the place where “you store the relevant information” of the several levels is the “stack” (128). The recursive game Danielewski engages in is, inter alia, the constant alternation between several levels by pushing and popping. Each time either Anwar or Astair opens a new parenthesis, they are pushing their utterance to a lower level that specifies their thoughts, through adjectives and adverbs for example, and by closing the parenthesis, they pop back, reverting to the original level. According to this definition, Xanther’s questions, which beget a swath of further questions branching off the original one, is in fact recursive as well, because they push the questions to more specific levels. Xanther’s forest is also a manifestation of that, since the term “recursive tree” is a well-known concept in graph theory, wherein visualizations of recursion often assume the shape of a tree; for Anwar and Astair, the “syntactic tree diagrams” would show similar shapes.
Besides TF-Narcon9, there are two other Narcons interfering in the narrative arc, namely TF-Narcon3 and TF-Narcon27. Like TF-Narcon9, they are distinguished by their unique fonts, and one can use this to trace a continuous, climactic thickening: TF-Narcon3 (Manticore) looks rather bony and fragile because it visibly displays its serifs, while TF-Narcon9 (MetaPlus-) appears to be overall thicker precisely due to being sans-serif, and TF-Narcon27 (Arial MT) seems, due to Arial’s famously high grey values, to be formatted in bold characters, and thus truly voluminous, as the number 27 has predicted ever so often. In the three fonts, then, one can almost trace the development from line, to plane, to volume, which is also reflected in the numbers: 3, 3 × 3 = 9, 3 × 3 × 3 = 27. Outside of their formal materialization on the page, the three Narcons are ostensibly bestowed with different analytical capacities, as TF-Narcon3 only appears to register what happens “in 3 dimensions,” while TF-Narcon9 provides accounts of the characters’ psychologies and thoughts, and TF-Narcon27 seems to have thoroughly supernatural knowledge concerning the future or the past. This can be compared to Edwin A. Abbott’s Flatland. A Romance of Different Dimensions (1884), in that the planar bodies, line and square, populate flatland while the voluminous body—in Abbott’s example the ball—enjoys a panoramic view of the plane and as such substantially more cognizant about the overall organization of life than the inhabitants of the plane, by which his knowledge and demeanor appears to be supernatural. Another way to illustrate this would be to reinvoke the image of the Rubik’s Cube: one can imagine TF-Narcon3 positioned outside of the cube, while TF-Narcon9 is positioned inside one of the sides, and TF-Narcon27 is the entire cube.
Therefore, Narcons appear to be “story machines” or computers that produce a textual string from different perspectives when fed the proper numbers. But they are by no means omniscient: we learn on multiple levels that Xanther’s psychology is beyond the numeric, defying the possibility of a comprehensive arithmetization; the Narcons confirm this by stating that “[b]y contrast, TF-Narcon9 X (TOTAL) is too vast to represent” (TFv1 568). Moreover, her empowerment through the indeterminate form of “1 = 2”, the cat-sum, reveals the impossibility to reduce her brain to computational laws as exemplified by Boolean algebra. Against this background, Xanther’s epilepsy, in the sense of an uncontrollable electrical mega-activity in her brain, can also be seen as a figurative rebellion against such a tendency to digitize: her brain is not only more than a computer but in fact more than the computational as such. It is thus logical that Xanther, transcending the orders of numbers especially since the cat-sum “1 = 2,” increasingly violates the rules of the numerically rigid “format” of The Familiar, which has, as of now, remained somewhat intact, but could be even more explicitly undermined in the future seasons.
Conclusion: Extrarithmetic
In times in which the computer is lifted into a cardinal position of quasi-omniscience and when big data and comprehensive statistics corroborate the mantra of the impeccability of the number, Danielewski’s arithmopoetics puts this ideology into question by contextualizing numbers from many different perspectives. I have argued that an arithmopoetics informs substantially both form and content, which I have labelled exorithmetic and endorithmetic, and furthermore function as a hinge between the two, which I have labelled mesorithmetic. Not only through its colossal form as a serial novel does The Familiar show that primarily staggering numbers have permeated many branches of Western culture, making the reader aware of many shortcomings and problems of assuming the primacy of the number. With examples including messages, calls, and spam attacks in information technology, financial bookkeeping, and the count of raindrops, the limits of the countability and computability of the world are tested, and the repercussions of such an information overload range from a headache to an epileptic attack.
Yet, Danielewski also shows foremost through Xanther that there is a principal barrier where any attempt of arithmetization must founder. As the Narcons confess:
Especially the last avowal attests that the numerical must resign in the face of the concept of raindrops, a phenomenon that, due to its fuzziness, may not even be countable in theory, let alone in practice. I have shown that Danielewski makes this clear through both signiconic conceits, which combine Danielewski’s arithmopoetics with his hallmark topopoetics, as well as discussions pertaining to the “muddiness” of the world. In the first volume of The Familiar, the transition from the mathematically to the dynamically sublime rainstorm portrays how the concept of countability becomes an increasingly inapt tool to make numerical sense of the rain: how could we even begin to define what a raindrop is, as it splashes, fuses, and divides ever so often? Correspondingly, the illegibility of the question “How many raindrops?” maps onto the uncountability of the drops. Xanther imagines that only “frozen rain” could render the project feasible, as this way all contours and forms are sustained. However, Danielewski also makes clear that counting raindrops this way is rather artificial and will never lead to an experience of rain; in other words, numbers cannot bridge the gap between raindrops and rain. Second, the discussion on the muddiness of the world, featured most prominently when Xanther reminisces about Dov, relates in many ways to this one-many problem. We have seen that each phenomenon can be taken to be “one” or “many,” yet the quick oscillation between the two is what disquiets Xanther.
I have further argued that Xanther’s epilepsy is the exacerbation of this feeling of uneasiness and that her epileptic shaking metaphorizes the conflict between order and chaos. On top of the rainy episodes, her epileptic fit at the ballet Hades in New York is evidence of this: too far away from Redwood, she suffers a seizure when she observes how quickly the demons transition from being caged and countable to roaming freely and being uncountable. The first season then resolves this predicament, when Xanther masters one of Anwar’s “indeterminate forms,”16 namely the arithmopoetic equation “1 = 2.” Under the laws of Boolean algebra and binary code this equation is nonsensical, but Danielewski features this equation as a paradoxical truth that settles the one-many-problem for Xanther, helping her transcend the problem of counting altogether. Through all of this, we see that Danielewski is not only fascinated by numbers, forms and formats, computer science and digitization, but at the very same time critical with respect to their scope, validity, and significance. On all levels, then, numbers may surely approach but never exhaust whatever object they describe; the fact that the Narcons “invalidate” the numerical format of the novel just as Xanther and Redwood “invalidate” the laws of arithmetic show that interpreting The Familiar means going beyond the scope of numbers, engaging in what could be termed extrarithmetic.
Lastly, I must add that some portions of this essay are only valid as long as this serial format is upheld. Writing an essay on the first season of an unfinished literary project is always afflicted with such dangers, prone to be collapsed by the next season. That might be the beauty and sadness of all literary essays that write into the yet unfinished work of an artist. Also, this essay has been written during the COVID-19 pandemic, and I must say that there is something familiar about the next season and the next morning: I cannot resist looking at the numbers again.
Notes
- Excerpt(s) from THE FAMILIAR, VOLUME 1: ONE RAINY DAY IN MAY by Mark Z. Danielewski, copyright © 2015 by Mark Z. Danielewski. Used by permission of Pantheon Books, an imprint of the Knopf Doubleday Publishing Group, a division of Penguin Random House LLC. All rights reserved. These images are not included under the Creative Commons License for this article. [^]
- A 2014 study conducted by bookwraiths.com has rank-ordered fantasy series by their page count. The #1 at that time was the 45-volume Discworld franchise by Terry Pratchett, which comprises 15,497 pages. In that ranking, Danielewski’s novel would be the undisputed #1, which indicates the unprecedented enormity behind the page-count of the project. [^]
- “And I began to see that it also made sense from my point of view as a creator, in that House Of Leaves was very much about a film, Only Revolutions is very much about music, and this is about a television series. Just a longform investment in the future” (NPR). For a more thorough analysis of The Familiar with respect to its “serial-like” makeup, consult van de Ven (2016). [^]
- Furthermore, obtaining the prime factorization of 27 = 3 × 3 × 3, it follows that it is neither divisible by 4 (season count of Battlestar Galactica), nor 5 (season count of Breaking Bad and The Wire), nor 6 (season count of The Sopranos), nor 7 (season count of Mad Men), which is somewhat at odds with the consistently fixed length of the internal structure of each volume. In other words, the 27 volumes cannot be grouped together in seasons of equal length, as there must be at least one longer season than the first two, which predicts that there cannot be an arithmetically “perfect” serialization. [^]
- The entire series would weigh a staggering 1655g × 27 = 44.685g, so approximately 44 kilograms. If somebody said that they took The Familiar with them on vacation, we could safely conclude that they referred to a digital form. [^]
- Without going into too much detail, a simple physical formula, the axial mass moment of inertia, measures the resistance of an object to rotational movement. The novels are here taken as cuboids, therefore the formula is
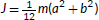 . For each novel, the formula yields
. For each novel, the formula yields
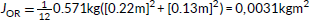
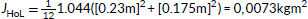
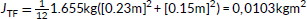 .
As a result, the amount of energy to be expended to rotate Only Revolutions, House of Leaves and The Familiar is very close to the ratio 1: 2: 3, in that order.
[^]
.
As a result, the amount of energy to be expended to rotate Only Revolutions, House of Leaves and The Familiar is very close to the ratio 1: 2: 3, in that order.
[^]
- Psychologists E. L. Kaufman et al., who coined the term subitize, highlight some similarities between subitizing and “estimating” or “grasping by intuition” (520) and some differences to “counting” (522). [^]
- Also note that the pink-colored dog-ears are present in those signiconic images in the subitizing range (TFv1 49, 51, 55) but vanish in the staggering range (TFv1 62-65, 67-68, 478-79, 494-95, 514-15), suggesting the presence of the infinite that may not be contained by conventional boundaries. [^]
- In mathematics, Laplace’s equation, also called the “equation of continuity,” expresses this idea that a fluid like mud is, in Astair’s words, “beyond defeat.” Laplace’s equation is:
 As Eric Temple Bell argues: “In fluid motion this is the mathematical expression of the fact that a ‘perfect’ fluid, in which there are no vortices, is indestructible” (104, my emphasis).
[^]
As Eric Temple Bell argues: “In fluid motion this is the mathematical expression of the fact that a ‘perfect’ fluid, in which there are no vortices, is indestructible” (104, my emphasis).
[^]
- A tragic moment occurs immediately afterwards, when Anwar’s aforementioned balance sheet of the household finances yields a ‘0,’ on which he comments: “That zero as round as happiness [surrounding and comforting his family {hard-pressed since they first moved here}]. Anwar could live with such a zero” (TFv1 84). Xanther mortification is thus not in the least shared by Anwar. Therein lies a tragedy because it is not communicated to the other person but only to the reader. [^]
- The limits of this present essay do not permit further analysis of the depictions of the epileptic in Poe. For further reading, consult Peter Wolf’s “Epilepsy and Catalepsy in Anglo-American Literature” (2000). [^]
- Dr. Brady and Tessara are sure that it is “no more than two weeks old. Maybe not more than one” (TFv1 827) and Astair mentions that he “looks like a kitten” (TFv2 103) at Dr. Syd Lactnod’s veterinary office, yet “the skin is nothing but little wrinkles” (TFv2 101) and the cat shows a “[h]eavy tartar buildup. Gums worn. Pigmentation too” (TFv2 103), all of which are signs of an advanced age. [^]
- One can follow and relive the discrete iterations of Arnold’s cat map, for example, on http://gerdbreitenbach.de/arnold_cat/cat.html. On that page, a red number on the top left corner of the image indicates the number of iterations. The interested reader is invited to find out how many iterations are necessary for the cat to recur. [^]
- Sascha Pöhlmann’s introduction to this special issue has already hinted at the connection between the character count and the lives of a cat: “On the narrative level, there are nine different strands centered around different protagonists during these few months, and the number is only the first of many cat-related allusions and puns.” As Pöhlmann further postulates that “finding out just how they might be connected is one of the major interpretive challenges of the novels,” the present arithmopoetic speculation may thus serve as one possible connection. [^]
- Pöhlmann argues that the vertical black bars that bracket the Narcon interruption resemble the “pause” symbol (cf. “Multimodalität” 288). [^]
- Note also that the phrase “indeterminate form” perfectly captures the problem of having contours and not having contours at the same time. [^]
Competing Interests
The author has no competing interests to declare.
References
Aarseth, Espen J. Cybertext. Perspectives on Ergodic Literature. Johns Hopkins University Press, 1997.
Aristotle. “Poetics.” The Complete Works of Aristotle, vol. 2. edited by Jonathan Barnes. Princeton University Press, 1984, pp. 2316–40. DOI: http://doi.org/10.1515/9781400835850-019
Arnold, Vladimir Igorevich, and André Avez. Ergodic Problems of Classical Mechanics. University of Paris, 1968.
Askin, Ridvan. “‘Folding, Unfolding, Refolding’: Mark Z. Danielewski’s Differential Novel House of Leaves.” Pöhlmann, Revolutionary Leaves, pp. 99–122.
Bekavac, Luca. “Matrix Pauoris. Material Dislocation in House of Leaves.” Essays on the Horrors of Speculative Philosophy, edited by Matt Rosen, Punctum Books, 2020, pp. 315–60. DOI: http://doi.org/10.2307/j.ctv19cwdpb.12
Bell, Eric Temple. Men of Mathematics. Simon & Schuster, 1937.
Berlinski, David. One, Two, Three: Absolutely Elementary Mathematics. Vintage, 2011.
Berressem, Hanjo. “The Surface of Sense, The Surface of Sensation and the Surface of Reference: Geometry and Topology in the Works of Mark Z. Danielewski.” Pöhlmann, Revolutionary Leaves, pp. 199–222.
Danielewski, Mark Z. House of Leaves. Pantheon, 2000.
Danielewski, Mark Z. Only Revolutions. Pantheon, 2006.
Danielewski, Mark Z. The Familiar. Vol 1–5. Pantheon, 2015–17.
Derrida, Jacques. The Truth in Painting, translated by Geoff Bennington and Ian McLeod, Chicago University Press, 1987. DOI: http://doi.org/10.7208/chicago/9780226807690.001.0001
Frege, Gottlob. The Foundations of Arithmetic, translated by J. L. Austin, Harper Brothers, 1950.
Greve, Julius. “Danielewski, or, Metacommentary as Literary Production.” Pöhlmann, Revolutionary Leaves, pp. 77–98.
Hofstadter, Douglas. Gödel, Escher, Bach: An Eternal Golden Braid. Basic Books, 1979.
Kant, Immanuel. Critique of the Power of Judgment, edited by Paul Guyer, translated by Paul Guyer and Eric Matthews, Cambridge UP, 2000. DOI: http://doi.org/10.1017/CBO9780511804656
Kaufman, E. L., et al. “The Discrimination of Visual Number.” The American Journal of Psychology, vol. 62, no. 4, University of Illinois Press, 1949, pp. 498–525. DOI: http://doi.org/10.2307/1418556.
Maturana, Humberto, and Francisco Varela. The Tree of Knowledge: The Biological Roots of Human Understanding. Shambhala Publications, 1992.
Rath, Arun. “Danielewski Returns With A Long, Sideways Look At ‘The Familiar.’” 2015. https://www.upr.org/post/danielewski-returns-long-sideways-look-familiar#stream/0
Schrödinger, Erwin. “The Present Situation in Quantum Mechanics.” Proceedings of the American Philosophical Society, vol. 124, no. 5, 1980, pp. 323–38.
Shapiro, Stewart. Thinking About Mathematics. Oxford University Press, 2000.
Stirling, Jeannette. Representing Epilepsy. Myth and Matter. Liverpool University Press, 2010. DOI: http://doi.org/10.5949/UPO9781846316173
Plato. “Parmenides.” Plato: Complete Works, edited by John M. Cooper, Hackett Publishing, 1997, pp. 349–98.
Poe, Edgar Allan. “Berenice.” The Complete Tales, pp. 227–33.
Poe, Edgar Allan. The Complete Tales and Poems of Edgar Allan Poe, Barnes & Noble, 2006.
Poe, Edgar Allan. “The Facts in the Case of M. Valdemar.” The Complete Tales, pp. 721–28.
Pöhlmann, Sascha. “Introduction: Becoming Familiar with The Familiar, or, The Imaginary Novel and the Imagination.” Mark Z. Danielewski’s “The Familiar,” special issue of Orbit: A Journal of American Literature, vol. 10, no. 2 (2022). DOI: http://doi.org/10.16995/orbit.8645.
Pöhlmann, Sascha. “Multimodalität als Grenzgang des Narrativen im Romanwerk Mark Z. Danielewskis.” META-Fiktionen. Der experimentelle Roman seit den 60er-Jahren. Ed. Wilhelm Haefs and Stefan Brückl. München: text + kritik, 2021, pp. 260–97.
Pöhlmann, Sascha. Revolutionary Leaves: The Fiction of Mark Z. Danielewski. Cambridge Scholars Publishing, 2012.
Pöhlmann, Sascha. “The Democracy of Two: Whitmanian Politics in Only Revolutions.” Pöhlmann, Revolutionary Leaves, pp. 1–32.
Pynchon, Thomas. Mason & Dixon. Vintage, 1998.
Wolf, Peter. “Epilepsy and Catalepsy in Anglo-American Literature between Romanticism and Realism: Tennyson, Poe, Eliot, and Collins.” Journal of the History of the Neurosciences, vol. 9, no. 3, 2000, pp. 286–93. DOI: http://doi.org/10.1076/0964-704X(200012)9:3;1-#;FT286